Простейшие свойства матричного формализма

1⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n), w = (w₁ , … , w_n) Î Vⁿ сложение ассоциативно: (u+v)+w = u+(v+w).

2⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n) Î Vⁿ сложение коммутативно: u+v= v+u.

3⁰. Существует нулевая к.с.в. 0 = (0, … , 0) Î Vⁿсо свойством нейтральности по сложению: для любой к.с.в v = (v₁ , … , v_n) Î Vⁿвыполнено 0+ v = v = v+ 0.

4⁰. Для любой к.с.в. v = (v₁ , … , v_n) Î Vⁿ существует противоположная к.с.в. –v = (–v₁ , … , –v_n) Î Vⁿ со свойством v+ (–v) = 0= (–v) + v.

5⁰. Для любой к.с.в. v = (v₁ , … , v_n) Î Vⁿ и матриц А Î M(n, k, F), B Î M(k, m, F) справедлив аналог ассоциативности: (v×A)×B = v×(A×B).

6⁰. Для единичной матрицы I_n Î M(n, F) и к.с.в. v = (v₁ , … , v_n) Î Vⁿ выполнено равенство v×I_n = v.

7⁰. Для любой к.с.в. v = (v₁ , … , v_n) Î Vⁿ и матриц А, B Î M(n, m, F) справедлив аналог дистрибутивности v×(A + B) = v×A + v×B.

8 ⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n) Î Vⁿ и матрицы А Î M(n, m, F) выполнен аналог дистрибутивного закона: (u+ v)×A = = u×A + v×A.

Доказательства этих свойств полностью аналогичны соответствующим доказательствам правил действия со строками и матрицами. Например, свойство 5⁰ можно доказать так: если v×A = u Î V^k, u×B = w Î V^m, A×B = C, v×C = x, то

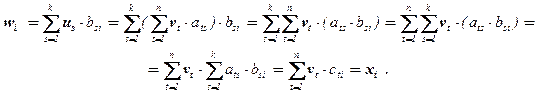
Отметим попутно, что первые четыре свойства означают, что множество Vⁿ всех n-элементных систем векторов является абелевой группой относительно введённой операции сложения к.с.в.

9⁰. Для любых к.с.в. u = (u₁ , … , u_n), v = (v₁ , … , v_n) Î Vⁿ и обратимой матрицы А Î GL(n, F) равенство u = v×A равносильно v = u×A^–1 .

Действительно, если u = v×A, то u×A^–1 = (v×A)×A^–1 = v×(A×A^–1) = v×I_n = v. Точно так же из равенства v = u×A^–1 выводится равенство u = v×A (?!).

10⁰. Для любой к.с.в. v = (v₁ , … , v_n) Î Vⁿ и матриц А, В Î M(n, m, F) равенство v×A = v×B равносильно равенству v×(A – B) = 0Î Vⁿ.

В самом деле, v×A = v×B Û (" j (1 £ j £ m) v×a^(j) = v×b^(j)) Û (" j (1 £ j £ m) v×(a^(j) – b^(j)) = 0 Î V) Û v×(A – B) = 0= (0, … , 0)Î Vⁿ.

Упражнения: 1. Докажите все перечисленные выше и ещё недоказанные свойства.

2. Определите для каждого a Î F такую унарную операцию a×умножения произвольной к.с.в. v = (v₁ , … , v_n) Î Vⁿ на любой скаляр a Î F, чтобы алгебра (Vⁿ, + , {a× | a Î F}) была векторным пространством над полем F.

3. Сформулируйте и докажите аналогичные свойства к.с.в.-столбцов.

Следующие свойства используют матричный символизм для выражения некоторых фактов о линейно зависимых и линейно независимых системах векторов.

11⁰. Имеет место эквивалентность: (к.с.в. v = (v₁ , … , v_n) Î Vⁿ линейно зависима) Û ($ a Î ⁿF \ {0} v×a = 0).

12⁰. Имеет место эквивалентность: (к.с.в. v = (v₁ , … , v_n) Î Vⁿ линейно независима) Û (" a Î ⁿF \ {0} v×a = 0 ® a = 0)

Оба этих свойства являются переформулировками определений линейной зависимости и независимости на матричном языке.

13⁰. Имеет место эквивалентность: (к.с.в. v = (v₁ , … , v_n) Î Vⁿлинейно независима) Û (" A, B Î M(n, m, F) v×A = v×B ® A = B)

(Þ) Если v линейно независима иv×A = v×B, то v×(A – B) = 0, т.е. (по 12⁰) все столбцы матрицы А – В нулевые, а значит А = В.

(Ü) следует из 12⁰ , если положить A = a , B = 0 .

14⁰. Имеет место эквивалентность: (e = (e₁ , … , e_n) – базис V) Û Û (" f = (f₁ , … , f_m) Î V^m $ ! T Î M(n, m, F) f = e×T)

(Þ) Поскольку e – базис, каждый вектор f_i однозначно записывается в виде линейной комбинации векторов системы e: f_i = t_i1×e₁ + … + t_in×e_n . Если T = (t_ij) – матрица с компонентами t_ij (1 £ i £ n, 1 £ j £ m ), то f = e×T. Такая матрица T определена однозначно: если f = e×T = e×S, то ввиду линейной независимости базиса e, свойство 13⁰ даёт T = S.

(Ü) Поскольку " v Î V $ t Î ⁿF v = t×e(применили условие для системы f = (v)), то L(e) = V. Кроме того, система e линейно независима: если e×t = 0 для некоторого t Î ⁿF, то e×t = 0= e×0 , и условие единственности матрицы T для к.с.в. f = {0} даёт t = 0 . Таким образом, e является базисом векторного пространства V.

15⁰. Пусть e = (e₁ , … , e_n) – базис векторного пространства V, f = e×T, где T Î M(m, n, F). Тогда ( f – базис V) Û (T – обратимая матрица, т.е. T Î GL(n, F))

(Þ) Если f = (f₁ , … , f_m) – базис, то n = m, т.к. базисы состоят из одного и того же числа векторов. Таким образом, T – квадратная матрица. Если она не обратима, то T – левый делитель нуля: $ x Î ⁿF \ {0} T×x = 0, и f×x = = e×T×x = e×0 = 0, вопреки линейной независимости к.с.в. f .

(Ü) Во-первых, к.с.в. fлинейно независима: если $ x Î ⁿF \ {0} f×x = 0 , то e×T×x =0 и ввиду линейной независимости базиса e получаем T×x = 0 , т.е. x = T ^–1×T×x = T ^–1×0 = 0 – противоречие.

Во-вторых, L(f) = V : если v Î V, то $ a Î ⁿF v = e×a,и значит, v = (e×T)×(T ^–1×a) = f×( T ^–1×a) = f×b, где b = T ^–1×a .