Матрица линейного оператора

Пусть V – векторное пространство с базисом e = (e₁ , … , e_n), j : V ® V – линейный оператор. Обозначим через j(e) конечную систему векторов (j(e₁), … , j(e_n)) Î V ⁿ. Каждый вектор j(e_j) (1 £ j £ n) к.с.в. j(e) однозначно записывается в виде j(e_j) = e×[j(e_j)]_eи из полученных координатных столбцов можно образовать матрицу [j]_e = ([j(e₁)]_e , … , [j(e₁)]_e ) Î M(n, F), которая называется матрицей линейного оператора j в базисе e и удовлетворяет равенству j(e) = e×[j]_e .

Примеры: 1. Пусть линейный оператор j : V ® V переводит базис e = (e₁ , e₂ , e₃) трёхмерного векторного пространства V в систему векторов (e₂ + e₃ , e₁ – e₂ , e₁ + e₃). Тогда [j(e₁)]_e = 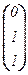, [j(e₂)]_e = 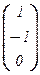, [j(e₃)]_e = 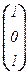,и [j]_e = .

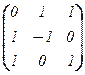2. Пусть V = R³, j : R³ ® R³ , j(x; y; z) = (x – y; y + z; x). Найдём матрицу [j]_e в базисе e = (e₁ = (1; 1; 0), e₂ = (0; 1; 1), e₃ = (0; 0; 1)).

Имеем j(e₁) = j(1; 1; 0) = (0; 1; 1), j(e₂) = j(0; 1; 1) = (–1; 2; 0), j(e₃) = = j(0; 0; 1) = (0; 1; 0). Искомая матрица линейного оператора j состоит из координатных столбцов полученных векторов. Поэтому получается матричное уравнение

(e₁^t , e₂^t , e₃^t)×[j]_e = (j(e₁)^t, j(e₂)^t, j(e₃)^t) или 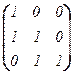×[j]_e = .

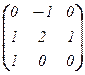Значит [j]_e = .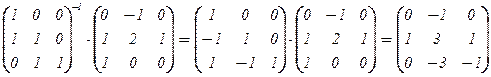

3. Матрица линейного оператора j : F ⁿ ® F ⁿ в базисе e = (e₁ , … , e_n) находится из матричного уравнения (e₁^t , … , e_n^t)×[j]_e = (j(e₁) ^t , … , j(e_n) ^t).

4.Матрица линейного оператора j : ⁿF® ⁿFв базисе e = (e₁ , … , e_n) находится из матричного уравнения (e₁ , … , e_n)×[j]_e = (j(e₁) , … , j(e_n)).