Матричный формализм в векторных пространствах

Пусть V– векторное пространство над полем F, n Î N. Любой упорядоченный набор v =(v₁, … , v_n) Î Vⁿ, или аналогичный упорядоченный набор-столбец или даже множество v = {v₁, … , v_n } Í V будем называть конечной системой векторов в пространстве V или кратко к.с.в. В каком именно виде будут возникать в дальнейшем к.с.в. зависит от контекста: к.с.в. в виде множества удобно использовать, если не существенен порядок рассматриваемых векторов; если же порядок важен для рассуждений, то будем использовать к.с.в. в виде строк или столбцов (в зависимости от специфики конкретной ситуации).

Пример: Пусть (–1; 2; 3), (3; 1; 1) Î R³. Тогда ((–1; 2; 3), (3; 1; 1)) Î (R³)², 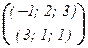Î ²(R³) , {(–1; 2; 3), (3; 1; 1)} Í R³ – конечные системы векторов.

Пусть v = {v₁ , … , v_n} – к.с.в. , a₁ , … , a_n Î F. Тогда линейную комбинацию векторов a₁×v₁+…+a_n×v_n Î Vудобно записывать, используя матричные обозначения. Так, если v = (v₁ , … , v_n) Î Vⁿ, a = 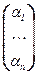Î ⁿF, то можно естественным образом определить результат умножения v×a “строки” v на столбец a как v×a = (v₁ , … , v_n)× 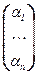= v₁×a₁+…+v_n×a_n = a₁×v₁+…+a_n×v_n Î V. Такая символика хорошо согласуется с обычными матричными обозначениями. В точности так же, если v = Î ⁿV, a = (a₁ ; … ; a_n) Î Fⁿ , то можно определить результат умножения a×v строки a на “столбец” v формулой a×v = (a₁ ; … ; a_n)× = a₁×v₁+…+a_n×v_n Î V. Таким образом, линейная комбинация векторов является результатом умножения векторной “строки” на скалярный столбец или скалярной строки на векторный “столбец”.

Матричный формализм можно расширить далее, распространив его на матрицы. Пусть v = (v₁ , … , v_n) Î Vⁿ, А Î M(n, m, F). Тогда определим результат умножения к.с.в. v на матрицу A как к.с.в. v×A = (u₁ , … , u_m) Î V^m, где u_i = v×a⁽ⁱ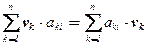⁾ = . Таким образом, каждый вектор к.с.в. u является результатом умножения строки v = (v₁ , … , v_n) на соответствующий столбец матрицы А .Аналогично определяется результат умножения матрицы A Î M(m, n, F) на к.с.в. v = : A×v = 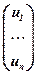Î ^mV, где компоненты u_iвычисляются естественно: u_i = a_i×v = .

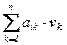Кроме того, условимся складывать две к.с.в. одинакового “размера” по обычному правилу: если v = (v₁ , … , v_n), u = (u₁ , … , u_n) Î Vⁿ , то полагаем v + u = (v₁ + u₁ , … , v_n + u_n). Аналогично определяется сложение к.с.в. в виде столбцов: если v = , u= 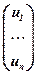Î ⁿV, то v+u = .