Координатная форма записи линейного оператора
Пусть V – векторное пространство над полем F с базисом e = (e1 , … , en), j : V ® V– линейный оператор, x Î V. Найдём связь между координатными столбцами [x]eи [j(x)]e .
Пример.Пусть F – поле, V = n F, A Î M(n, F). Тогда отображение m : n F ® n F, заданное правилом " x Î n F m(x) = A×x , является линейным оператором, причём для стандартного базиса e = (e1t , … , ent) в n F,гдеei = (0; … ; 0; 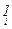 , 0; … ; 0), имеем [x]e = xи m(x)]e = [A×x]e = A×x = [m]e . Таким образом, " x Î n F [m(x)]e = [m]e×[x]e.
, 0; … ; 0), имеем [x]e = xи m(x)]e = [A×x]e = A×x = [m]e . Таким образом, " x Î n F [m(x)]e = [m]e×[x]e.
Оказывается, что аналогичная формула имеет место и в общем случае. Для её вывода понадобится следующее свойство линейных операторов:
Свойство согласованности матричного умножения с действием линейного оператора: Пусть V – векторное пространство над полем F, j : V ® V – линейный оператор. Тогда для любой к.с.в v = (v1 , … , vn) Î Vn и матрицы T Î M(n, m, F) справедливо равенство j(v×T) = j(v)×T.
Действительно, если t(j) = 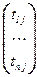 – j-й столбец матрицы T (1 £ j £ m), то
– j-й столбец матрицы T (1 £ j £ m), то
v×t(j) = t1j×v1+ … +tnj×vn , j(v×t(j)) = j(t1j×v1+ … +tnj×vn) =
= t1j×j(v1)+ … +tnj×j(vn) = j(v)×t(j).
Таким образом, j(v×T) = j(v1×t(1), … , vn×t(m)) = (j(v×t(1)), … , j(v×t(m))) = = (j(v)×t(1), … , j(v)×t(m)) = j(v)×T, что и требовалось доказать.
Теперь вывод общей формулы прост: если x = e×[x]e , то
e×[j(x)]e = j(x) = j(e×[x]e ) = j(e)×[x]e= e×[j]e×[x]e ,
так что [j(x)]e = [j]e×[x]e .
Доказанная формула [j(x)]e = [j]e·[x]e называется координатной формой записи линейного оператора j в базисе e.
Изменение матрицы линейного оператора при переходе
От базиса к базису
Пусть линейный оператор j : V ® V в векторном пространстве V имеет матрицу [j]e в базисе e = (e1 , … , en). Выясним, как изменится эта матрица при переходе к новому базису f = (f1 , … , fn).
Имеем j(e) = e×[j]e , j(f) = f×[j]f , f = e×Te, f . Поэтому j(f) =f×[j]f = = e×Te, f ×[j]f и j(f) = j(e×Te, f) = j(e)×Te, f = e×[j]e×Te, f . Значит Te, f ×[j]f = = [j]e×Te, f и (учитывая обратимость матрицы перехода Te, f) получаем
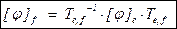 .
.
Пример. Пусть j : F3 ® F3 – линейный оператор, имеющий в базисе e = (e1 , e2 , e3) матрицу [j]e . Найдём [j]f, если
f = (e1 – e3 , e1 + e2 , 2×e2 + e3).
Имеем Te, f = 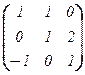 , Te, f–1 =
, Te, f–1 = 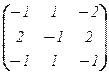 ,так что получаем по формуле [j]f =
,так что получаем по формуле [j]f = 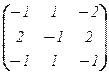 ×[j]e×
×[j]e× 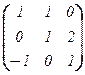 .
.
Дата добавления: 2021-12-14; просмотров: 397;











