Простейшие свойства линейных операторов

Всюду в дальнейшем (V , +, {a× | a Î F} ) и (W , Å , {aÄ | a Î F} ) – два векторных пространства над одним и тем же полем F, j : V ® W – линейный оператор.

1⁰. " n Î N" v₁ , … , v_n Î V " a₁ , … , a_n Î F

j(a₁×v₁+…+a_n×v_n)=a₁Äj(v₁)Å…Åa_nÄj(v_n)

Это доказывается индукцией по n, используя условия линейности и однородности.

2⁰. j(0_V) = 0_W

Действительно, ввиду свойства аддитивности имеем

j(0_V) + j(0_V) = j(0_V+0_V) =j(0_V) = j(0_V) + 0_W ,

откуда, сокращая обе части на j(0_V) в группе (W, +), получим требуемое равенство.

3⁰. " v Î V j(–v) = 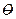j(v)

В самом деле, по условию аддитивности имеем

j(v) Å j(–v) = j(–v) Å j(v) = j(0_V) = 0_W.

4⁰. Если j : V ® W – мономорфизм, а u = (u₁ , … , u_n) – линейно независимая система векторов векторного пространства V , то система векторов j(u) = (j(u₁) , … , j(u_n)) является линейно независимой в пространстве W.

Действительно, если a₁Äj(u₁)Å…Åa_nÄj(u_n) = 0_W, то

j(a₁×u₁+…+a_n×u_n) = a₁Äj(u₁)Å…Åa_nÄj(u_n) = 0_W = j(0_V),

откуда (ввиду инъективности j) получаем a₁×u₁+…+a_n×u_n = 0_V. Значит по условию a₁ = … = a_n = 0, что и требовалось доказать.

5⁰. Если j : V ® W – эпиморфизм, а u = (u₁ , … , u_n) – система порождающих векторного пространства V, то j(u) = (j(u₁) , … , j(u_n)) является системой порождающих векторного пространства W.

В самом деле, для любого w Î W найдётся (ввиду сюръективности j) вектор v = a₁×u₁+…+a_n×u_n Î V со свойством w = j(v) = j(a₁×u₁+…+a_n×u_n) = = a₁Äj(u₁)Å…Åa_nÄj(u_n), что и требовалось.

6⁰. Любой изоморфизм векторных пространств отображает линейно независимые системы векторов в линейно независимые, а системы порождающих – в системы порождающих. В частности любой изоморфизм векторных пространств отображает базисы одного пространства в базисы другого.

Следует из 4⁰ и 5⁰.

7⁰. Пусть j : V ® W и y : V ® W – два линейных оператора и дан базис e = (e₁ , … , e_n) векторного пространства V. Если j(e_i) = y(e_i) (1 £ i £ n), то j = y. Другими словами, линейный оператор полностью определяется значениями на базисных векторах.

Если v = a₁×e₁ + … + a_n×e_n Î V, то

j(v) = j(a₁×e₁ + … + a_n×e_n) = a₁Äj(e₁) + … + a_nÄj(e_n) =

= a₁Äy(e₁) + … + a_nÄy(e_n) = y(a₁×e₁ + … + a_n×e_n) = y(v).

Поэтому отображения j и y совпадают.

8⁰. Пусть e = (e₁ , … , e_n) – базис векторного пространства V, а w₁ , … , w_n – произвольные векторы из W. Тогда существует единственный линейный оператор j : V ® Wсо свойством j(e_i) = w_i (1 £ i £ n).

Единственность линейного оператора со сформулированным свойством следует из свойства 7⁰. Докажем существование. Любой вектор v Î Vоднозначно раскладывается по базису e : v = a₁×e₁ + … + a_n×e_n. Поэтому формула j(v) = a₁Ä w₁ + … + a_nÄ w_n однозначно определяет отображение j : V ® W. Проверим, что j – линейный оператор.

(А): " x, y Î V j(x+ y) = j(x)Åj(y)

Если x = a₁×e₁+ … +a_n×e_n , y = b₁×e₁+ … +b_n×e_n , то

x + y = (a₁+b₁)×e₁+ … +(a_n+b_n)×e_n ,

j(x) = a₁Ä w₁+ … +a_nÄ w_n , j(y) = b₁Ä w₁+ … +b_nÄ w_n,

j(x+ y) = (a₁+b₁)Ä w₁+ … + (a_n+b_n)Ä w_n =

= (a₁Ä w₁+ … +a_nÄ w_n) + (b₁Ä w₁+ … +b_nÄ w_n) = j(x) + j(y).

(O): " x Î V " a Î V j(a×x) = aÄj(x)

Если x = a₁×e₁+…+a_n×e_n, то

j(a×x) = j((a×a₁)×e₁+…+(a×a_n)×e_n) = (a×a₁)Ä w₁+…+(a×a_n)Ä w_n =

= aÄ(a₁Ä w₁+…+a_nÄ w_n) = aÄj(x).

Таким образом, j удовлетворяет условиям аддитивности и однородности, т.е. является линейным оператором.

9⁰. Если j : U ® V и y : V ® W – два линейных оператора, то их композиция yoj : U ® W будет линейным оператором, называемым произведением линейных операторов j и y.

Нужно проверить линейность и однородность для y o j .

Аддитивность: " u₁ , u₂Î U yoj(u₁ + u₂) = yoj(u₁) + yoj(u₂) .

Действительно, yoj(u₁ + u₂) = y(j(u₁ + u₂)) = y(j(u₁) + j(u₂)) = = y(j(u₁)) + y(j(u₂))) = yoj(u₁) + yoj(u₂) .

Однородность: " u Î U " a Î F yoj(a×u) = aÄ (yoj(u)) .

В самом деле, yoj(a×u) = y(j(a×u)) = y(a*j(u)) = aÄ (y(j(u))) = = aÄ (yoj(u)).

В качестве следствия немедленно получается следующее свойство:

10⁰. Композиция мономорфизмов – мономорфизм, композиция эпиморфизмов – эпиморфизм, композиция изоморфизмов – изоморфизм.

11⁰. Если j : V ® W и y : V ® W – два линейных оператора, то отображение s : V ® W, заданное правилом " v Î V s(v) = j(v) Å y(v) является линейным оператором, называемым (поточечной) суммой линейных операторов j и y и обозначаемым через j Å y.

Нужно проверить свойства аддитивности и однородности.

(А): " x, y Î V s(x+ y) = s(x)Å s(y)

Имеем s(x+ y) = j(x+ y) Å y(x+ y) = (j(x) Å j(y)) Å (y(x) Å y(y)) = = (j(x) Å y(x)) Å (j(y) Å y(y)) = s(x)Å s(y).

(O): " x Î V " a Î V s(a×x) = aÄ s(x)

В самом деле, s(a×x) = j(a×x)Å y(a×x) = aÄj(x)Å aÄy(x) =

= aÄ (j(x)Å y(x)) = aÄ s(x).

Итак, s – линейный оператор.

12⁰. Если j : V ® W– линейный оператор, а l Î F – произвольный скаляр, то отображение h : V ® W , заданное правилом " v Î V h(v) = lÄj(v) является линейным оператором, называемым (поточечным) произведением линейного оператора j на скаляр l и обозначаемым через lÄ j .

Доказательство аналогично предыдущим.

13⁰. Если j : V ® W – изоморфизм векторных пространств, то обратное отображение j ^–1 : W ® V также является изоморфизмом векторных пространств.

Нужно проверить только гомоморфность отображения j ^–1 , т.к. его биективность следует из биективности отображения j .

Линейность: " w₁,w₂ Î W j ^–1(w₁ Å w₂) = j ^–1(w₁) + j ^–1(w₂).

В самом деле, если w₁ ,w₂ Î W , то (ввиду эпиморфности j) найдутся v₁ , v₂ Î V со свойством w_i = j(v_i) (i = 1, 2). Поэтому w₁ Å w₂ = j(v₁) Å j(v₂) = = j(v₁ + v₂) и (по определению обратного отображения j ^–1) j ^–1(w₁ Å w₂) = = v₁ + v₂ = j ^–1(w₁) + j ^–1(w₂) .

Однородность:" wÎ W " a Î F j ^–1(a Ä w) = a×j ^–1(w).

Действительно, если w Î W , то (ввиду эпиморфности j) найдётся v Î V со свойством w = j(v). Поэтому a Ä w = a Ä j(v) = j(a×v) и (по определению обратного отображения j ^–1) j ^–1(aÄ w) = a×v = a×j ^–1(w) .