Кинетическая энергия твердого тела

Твердое тело является частным случаем механической системы и рассматривается как непрерывно распределенная масса, тогда все суммы, входящие в выражение для кинетической энергии системы, переходят в интегралы. Так, для твердого тела формула (5.11) примет вид

Рис. 5.8

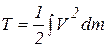. (5.14)

1. Кинетическая энергия твердого тела, двигающегося поступательно.

При этом виде движения скорости всех точек тела одинаковы (рис. 5.8). Вынося 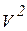в формуле (5.14) за знак интеграла, получим

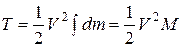. (5.15)

Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела M на квадрат его скорости.

2. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси

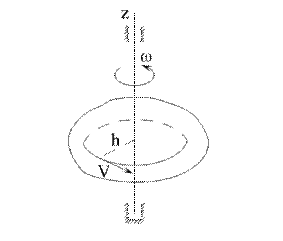Рис. 5.9

Модуль скорости V любой точки твердого тела, вращающегося вокруг неподвижной оси, равен 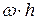, где 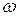- модуль угловой скорости твердого тела, 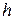- расстояние от точки до оси вращения z (рис. 5.9). Подставляя 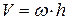в формулу (5.14), получим

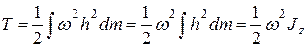(5.16)

здесь 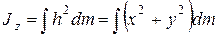– момент инерции твердого тела относительно оси z.

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.

3. Кинетическая энергия твердого тела при плоско – параллельном движении

При плоско – параллельном движении скорость любой точки тела состоит из геометрической суммы скорости полюса и скорости точки при вращении вокруг полюса. Пусть тело движется плоско в плоскости Oxy, тогда 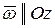. За полюс выбираем центр масс тела, тогда в формуле (5.13), скорость 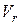есть скорость точки k тела при ее вращении относительно полюса (центра масс) и равна 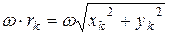, где 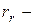расстояние k-ой точки до полюса. Тогда (5.13) перепишется

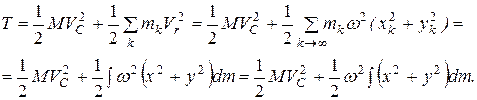
Имея в виду, что 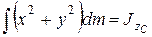– момент инерции тела относительно оси z, проходящей через полюс С, последнее выражение можно переписать как

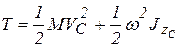, (5.17)

при плоско – параллельном движении тела кинетическая энергия складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.