Теорема об изменении кинетической энергии точки

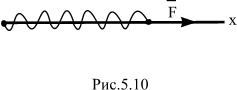
Найдем связь между работой и изменением скорости. Пусть материальная точка массой m перемещается вдоль оси Ох под действием силы, например сжатой или разжатой пружины, закрепленной в начале координат, – точке О (рис. 5.10). Уравнение движения точки имеет вид

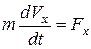. (5.18)

Умножим обе части этого уравнения на 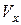, и, учитывая, что 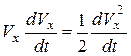, получим

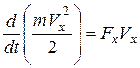. (5.19)

В правой части этого равенства заменим V_x на 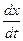и умножим на dt правую и левую части. Тогда

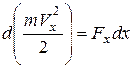. (5.20)

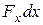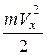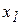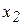В этом виде равенство имеет очень наглядный смысл: при смещении точки на dx, сила совершает работу , в результате чего изменяется величина кинетической энергии точки , характеризующая движение точки и, в частности, модуль ее скорости. Если точка смещается из положения в , а ее скорость при этом изменяется от 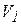до 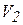, то, интегрируя (5.20), имеем

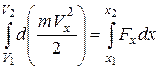. (5.21)

Учитывая, что 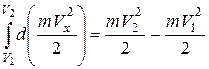, окончательно находим

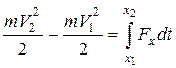. (5.22)

Изменение кинетической энергии материальной точки при ее каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.

При рассмотрении общего случая движения точки надо вместо уравнения проекций на ось (5.18) взять векторное уравнение движения

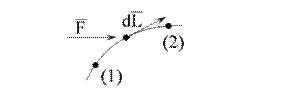Рис. 5.11

.

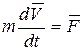Проделывая все предыдущие процедуры, получим

,

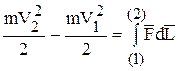здесь 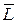– дуга, вдоль которой перемещается точка (рис. 5.11).