Элементарная работа сил, приложенных к твердому телу
Рассмотрим движение тела в плоскости. Пусть О – произвольно выбранная точка на твердом теле (рис.5.4). Назовем ее полюсом. Тогда движение тела в плоскости можно представить как сумму простейших: поступательного движения вместе с полюсом и вращение тела вокруг полюса. Тогда, скорость 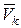 точки
точки 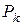 относительно неподвижной системы координат
относительно неподвижной системы координат  определится как геометрическая сумма двух скоростей
определится как геометрическая сумма двух скоростей
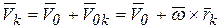 ,
,
где 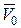 - скорость полюса,
- скорость полюса, 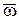 - вектор угловой скорости твердого тела,
- вектор угловой скорости твердого тела, 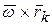 – скорость точки, при ее ращении вокруг полюса.
– скорость точки, при ее ращении вокруг полюса.
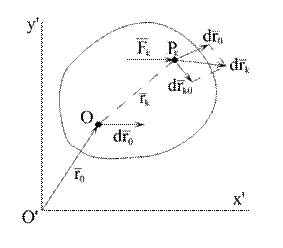 Рис. 5.4
Рис. 5.4
|
Будем представлять твердое тело как механическую систему, состоящую из N отдельных точек, взаимное расстояние между которыми не изменяется.
Вычислим смещение 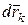 точки
точки 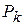 под действием силы
под действием силы 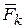 :
:
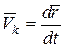 , тогда
, тогда 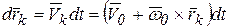 .
.
Элементарная работа, согласно (5.1), запишется следующим образом
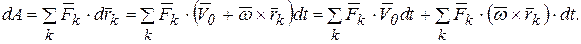
Воспользовавшись свойствами смешенного произведения векторов 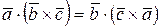 , перепишем последнее выражение в виде
, перепишем последнее выражение в виде
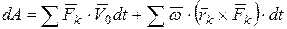 . (а)
. (а)
Пусть 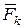 - равнодействующая всех сил, внешних и внутренних (рис5.4), приложенных в точке
- равнодействующая всех сил, внешних и внутренних (рис5.4), приложенных в точке 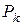 тела, т.е.
тела, т.е.
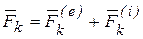 .
.
Тогда (а) запишется так
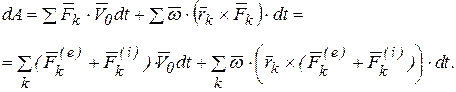
Согласно (3.1 и 3.2), главный вектор и главный момент внутренних сил системы равны нулю, получаем
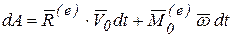 , (5.6)
, (5.6)
здесь: 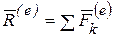 - главный вектор,
- главный вектор, 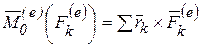 - главный момент внешних сил относительно точки О.
- главный момент внешних сил относительно точки О.
Частные случаи
A. Поступательное движение твердого тела. Все точки тела имеют одинаковые перемещения (рис. 5.5, а) и по модулю, и по направлению, тогда, из (5.6), получим (здесь 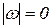 ):
):
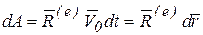 . (5.7)
. (5.7)
B. Вращение твердого тела вокруг неподвижной оси. Пусть ось z проходит через полюс О (рис. 5.5б). Тогда 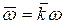 ,
, 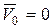 ; из (5.6) получим
; из (5.6) получим
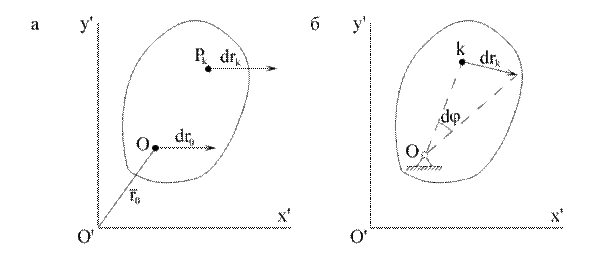 Рис. 5.5
Рис. 5.5
|
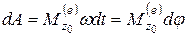 . (5.8)
. (5.8)
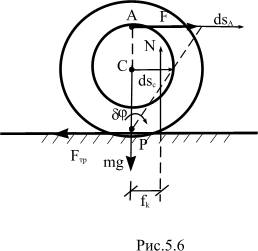
Пример. Катушка массой m и радиусом R приводится в движение постоянной силой F, приложенной в точке А (рис. 5.6). Катушка катится вправо без скольжения по шероховатой поверхности.
|
Вычислить работу всех внешних сил, если центр катушки переместился на расстояние 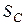 ,
, 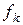 - коэффициент трения качения,
- коэффициент трения качения, 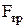 - сила трения, r – радиус сердечника катушки, к которой приложена сила.
- сила трения, r – радиус сердечника катушки, к которой приложена сила.
Решение. Катушка совершает плоское движение. Так как качение происходит без скольжения, то мгновенный центр скоростей находится в точке касания катушки с плоскостью, т.е. в точке Р (рис.5.6). Направим ось S по горизонтали вправо. В соответствии с направлением движения примем положительное направление угла поворота 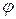 против хода часовой стрелки.
против хода часовой стрелки.
Пусть центр катушки С переместится на 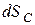 . При этом катушка повернется на угол
. При этом катушка повернется на угол 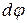 . Тогда
. Тогда 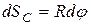 , откуда
, откуда
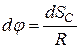 .
.
Приняв точку Р за мгновенную ось вращения, вычислим элементарную работу по формуле (5.8):
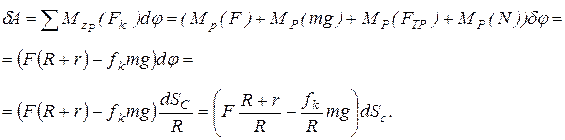 (а)
(а)
Здесь: линии действия сил 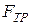 и mg пересекают ось вращения, поэтому
и mg пересекают ось вращения, поэтому 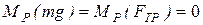 ; далее
; далее 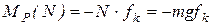 , где N – сила нормальной реакции.
, где N – сила нормальной реакции.
Для определения искомой работы остается взять определенный интеграл от (а) в пределах от 0 до SА. Получим
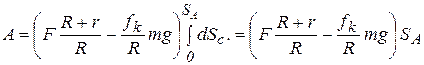 .
.
Дата добавления: 2019-12-09; просмотров: 861;











