Аксиома V. Равновесие нетвердого (деформируемого) тела не нарушится от затвердевания данного тела.

Эта аксиома известна в механике как принцип отвердевания.

Представим себе два тела А и В, которые имеют одинаковую форму, размеры и загружены одинаковыми системами сил , , 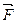,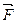…, 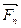. Положим, что одно из тел, например тело А нетвердое, а второе тело В является твердым. Смысл аксиомы V состоит в том, что если нетвердое тело А под действием системы сил находится в равновесии, то и твердое тело В под действием той же системы сил будет находиться в равновесии.

Эта аксиома широко используется в сопротивлении материалов. Она позволяет деформируемые или изменяемые тела, например, трос, гибкую балку, нить, цепь и т.п. рассматри­вать как твердые при определении влияния на них других тел или отдельных элементов друг на друга с использованием условий равно­весия статики.

Связи, их кинематические и статические

Характеристики.

Устройства, которые ограничивают свободу перемещения рассмат­риваемого тела в пространстве или на плоскости называются связями.

Связи могут быть удерживающими и неудерживающими, а также одно­сторонними и двухсторонними. Для установления характера связи необ­ходимо сместить тело в разных направлениях. Если при таком смеще­нии связь не покидает тело, то она является удерживающей. Если же тело при его смещении отделяется от связи, то она является неудерживающей. Примером удерживающей связи может служить проволока с натянутым на неё кольцом, а примером неудерживающей связи - опор­ная плоскость.

Каждая связь препятствует свободному смещению тела в одном или в нескольких направлениях на плоскости или в пространстве, т.е. уменьшает число степеней свободы данного тела. Под числом степе­ней свободы в механике следует понимать число независимых парамет­ров, которые определяют положение тала на плоскости или в простран­стве. Абсолютно твердое тело на плоскости имеет три, а в простран­стве шесть степеней свободы. Материальная точка обладает двумя степенями свободы на плоскости и тремя в пространстве.

Связи, наложенные на тело, могут быть простыми и составными. Простая связь препятствует смещению тела только в одном направле­нии, т.е. отбирает у него одну степень свободы. Составная связь препятствует свободному перемещению тела в двух или трех направле­ниях, а также свободному повороту вокруг одной или нескольких координатных осей. Составную связь всегда можно представить в ви­де системы определенного числа простых связей.

Загруженное тело действует на связи с определенными силами, которые называют активными. Одновременно с этим связи действуют на рассматриваемое тело с силами, направленными противоположно ак­тивным и равным им по модулю. Такие силы называются реактивными, или реакциями связей. Реакция является статической характеристикой связи. Она действует в том направлении, в котором связь препятст­вует перемещению тела. Таким образом, существует прямая зависимость между статическими и кинематическими характеристиками связей. Реакции связей возникают только при действии на тело за­данных активных сил. При разгрузке тела реакции связей исчезают.

В технической механике существует большой класс задач, требую­щих определения величин и направлений реактивных сил, которые воз­никают в связях загруженных тел. Что касается точек приложения реакций к телу, то они являются известными. Это точки закрепления тела, или точки контакта тела со связями. Неизвестными параметра­ми реакций связей, как правило, являются их модули и нап­равления.

Решение таких задач осуществляется на основании принципа освобождения от связей. Его сущность состоит в том, что заданное несвободное тело мысленно освобождается от связей, а их действие компенсируется приложением неизвестных реакций. При этом линии их действия совпадают с теми направлениями, по которым связи препят­ствуют свободным смещениям тела. Величины и направления неизвест­ных реакций устанавливаются из условий равновесия системы сил. Такие условия будут установлены в последующих главах.

Рассмотрим несколько примеров простых и составных связей твер­дого тела и укажем их кинематические и статические характеристики.

1. Тело опирается на гладкую плоскость в точке А (рис.1.8). Рассматриваемая плоскость является простой, и к тому же односторонней, связью тела. Она пре­пятствует свободному смещению тела вертикально вниз. Строго в этом направлении тело действует на плоскость с силой собственного веса 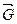. Со своей стороны гладкая плоскость действует на тело с силой 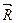, ко­торая является её реакцией.

Реакция 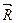, приложена в точке касания тела с плоскостью и направлена вдоль внешней нормали, проведенной к плоскости из точки касания.

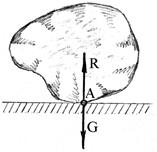
Рис.1.8

Если, к примеру, стержень (тело пра­вильной геометрической формы) опирается на

две гладкие плоскости в точках А и В (рис.1.9), то реакции 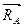и направлены перпендику­лярно опорным плоскостям и приложены к стержню в опорных точках А и В соответственно.

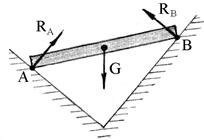
Рис.1.9

2. Простая опора. Если стержень опирается на неподвижную ли­нию, например, на ребро А двугранного угла (рис.1.10), то такая опо­ра стержня называется простой. Она препятствует смещению стержня в направлении, перпендикулярном к его поверхности.

Поэтому реакция такой опоры приложена в средней точке участка опирания и всегда направлена перпендикулярно к поверхности стержня (тела) в единственно возможном направлении - от опоры к стержню. В против­ном случае стержень покинет опору.

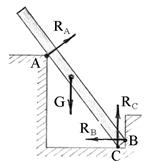
Рис.1.10

3. Связью тела является гибкая нить или шарнирно закреплен­ный стержень(рис.1.11,а и 1.11,б).

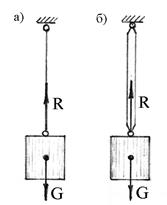
Рис.1.11

Под действием веса 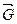, рассматриваемого тела в гибкой нити, или опорном стержне возникает реакция, которая направлена вдоль геометрической оси нити (стержня), так как только в этом направле­нии указанные связи препятствуют свободному перемещению тела.

4. Связью тела является цилиндрический шарнир. Конструктивно такая связь образуется из втулки и валика (рис.1.12). Втулка жест­ко соединяется с рассматриваемым телом, а валик соединяется с другими телами, неподвижными или подвижными. В первом случае шарнир­ную опору называют неподвижной, а во втором случае - подвижной. Предполагается, что поверхности валика и втулки абсолютно гладкие и втулка может свободно вращаться вокруг валика. В зависимости от расположения активных сил, реакция неподвижной шарнирной опоры мо­жет иметь различное направление, но линия её действия всегда про­ходит через центр валика. Следовательно, реакция шарнира имеет ра­диальное направление, т.е. нормальное к поверхности валика. Неиз­вестными являются численная величина реакции 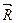и угол αмежду положительными направлениями координатной оси x и искомой реакции (рис.1.12,а).

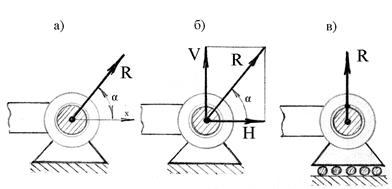
Рис.1.12

Неподвижный цилиндрический шарнир можно рассматривать как сос­тавную связь, препятствующую свободным перемещениям тела в двух взаимно перпендикулярным направлениям, совпадающих с направлениями координатных осей.

Тогда реакция 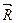. неподвижной шарнирной опоры будет определяться двумя составляющими: горизонтальной 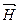и вертикальной 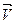, модули которых неизвестны и подлежат определению (рис.1.12,б).

Подвижный цилиндрический шарнир препятствует смещению тела лишь в одном направлении, перпендикулярном к направлению подвиж­ности опоры. В сторону внешней нормали к поверхности скольжения опоры направлена реакция 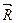подвижного шарнира (рис.1.12,в).

Более полный анализ составных связей и их реакций будет рассмотрен в главе V при изучении равновесия стержня и стержневых систем.

Вопросы для самоконтроля полученных знаний.

1) Что такое векторная и что такое скалярная величины?

2) Что такое сила в механике, и какими элементами она определяется?

3) Что принимается за единицу измерения силы в системе единиц СИ и в технической системе МКГСС?

4) Что представляет собой система сил, действующих на тело?

5) В каком случае две системы сил являются статически эквивалентными?

6) Что такое внешние силы, действующие на тело? Какие виды внешних сил могут быть приложены к телу?

7) Сформулируйте основные аксиомы статики.

8) Как определяется равнодействующая двух сил, приложенных в одной точке тела?

9) Что такое «действие» и «противодействие» двух тел?

10) Что такое свободное и несвободное тело?

11) Как называют устройства, ограничивающие свободу перемещения тел?

12) Какие виды этих устройств встречаются?

13) Что называют реакциями связей тела?

14) Как устанавливаются направления и линии действия реакций опорных связей тела?

15) Как направлены реакции гибкой нерастяжимой нити и жесткого стержня?

16) Как направлена реакция плоскости, если тело опирается на неё в одной точке?

17) Как направлена реакция связи в виде двухгранного угла, если на неё опирается плоское тело?

18) Что такое неподвижная цилиндрическая опора и как действует её реакция?

19) На какие составляющие может быть разложена реакция неподвижной цилиндрической опоры?

20) Что такое подвижная цилиндрическая опора и как действует её реакция?

ГЛАВА II

ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ.