Силовое поле. Силовая функция. Потенциальная энергия
Предположим, что точка движется в некотором пространстве и на нее со стороны пространства действует сила, которая зависит от положения точки в этом пространстве, но не зависит от скорости движения точки. В этом случае говорят, что в пространстве задано силовое поле, а также, что точка движется в силовом поле. Соответствующие понятия для системы материальных точек аналогичны.
Силы, зависящие от положения точек их приложения, в механике встречаются часто. Например, сила упругости, приложенная к материальной точке, которая движется по горизонтальной прямой под действием пружины. Важнейшим примером силового поля в природе является гравитационное поле: действие Солнца на планету данной массы определяется в каждой точке пространства законом всемирного тяготения.
Силовое поле называется потенциальным, если существует скалярная функция U, зависящая только от координат 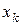 ,
, 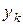 ,
, 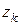 точки
точки 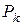 -точки материальной системы (возможно, и от времени), такая, что
-точки материальной системы (возможно, и от времени), такая, что
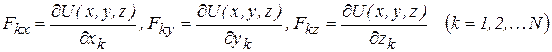 . (5.9)
. (5.9)
Функция 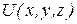 называется силовой функцией.
называется силовой функцией.
Рассмотрим свойства силовой функции.
Элементарная работа (5.1) связана с силовой функцией следующим образом
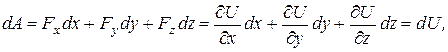
т.е. 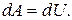
Таким образом, элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции.
Полная работа силы 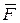 на участке от точки
на участке от точки 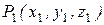 до точки
до точки 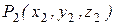 (рис.5.1)
(рис.5.1)
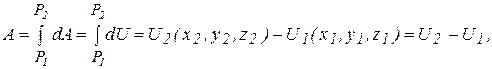
т.е. 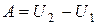 . (5.10)
. (5.10)
Из полученных выражений следует, что
1. работа силы в потенциальном силовом поле по любому замкнутому пути равна нулю;
2. работа силы в потенциальном силовом поле зависит только от положения конечной и начальнойточек, но сам путь перемещения роли не играет.
Потенциальная энергия. Потенциальной энергией П в рассматриваемой точке силового поля Р называют работу, которую совершают силы поля, действующую на материальную точку при ее перемещении из точки Р в начальную точку 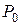 1, т.е.
1, т.е.
П= 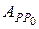 или П=
или П= 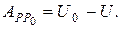
Свяжем силовую функцию U с потенциальной энергией. Имеем
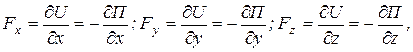
т.е.
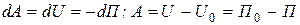 , или
, или 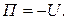
Примеры вычисления потенциальной энергии
1. Однородное поле тяжести. Пусть m – масса точки; g – ускорение свободного падения. Тогда (рис. 5.2)
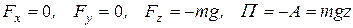 .
.
2. Силовое поле упругой пружины. Пусть материальная точка движется вдоль оси Ох (рис. 5.3) под действием пружины, к которой она прикреплена. Если при 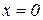 пружина не деформирована, то, полагая в формуле (5.5)
пружина не деформирована, то, полагая в формуле (5.5) 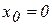 , получим
, получим
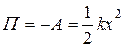 .
.
Дата добавления: 2019-12-09; просмотров: 806;











