Закон сохранения кинетической энергии

Для механической системы имеем

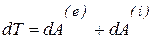, (5.26)

т.е. приращение кинетической энергии системы за конечное время равно работе всех сил системы за то же время.

Пусть все силы системы (внутренние и внешние) потенциальны, и их потенциал 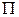не зависит явно от времени. В этом случае элементарная работа сил системы (п. 5.2.) будет полным дифференциалом

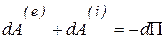тогда из (5.26) следует, что

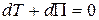Сумма кинетической и потенциальной энергии называется полной механической энергией системы. Из последнего равенства следует, что

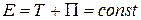, (5.27)

Равенство (5.27) называется интегралом движения, т.е. если все силы системы потенциальны и потенциал не зависит от времени, то при движении системы ее полная механическая энергия постоянна. Это закон сохранения механической энергии.

Следует иметь в виду, что для справедливости закона сохранения механической энергии требование о том, чтобы все силы системы были потенциальными, необязательно. Достаточно потребовать, чтобы потенциальными были силы, работа которых на действительном перемещении системы отлична от нуля.

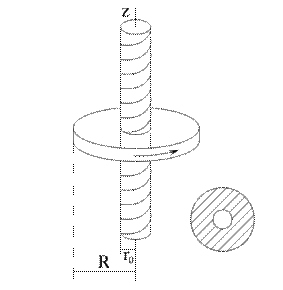Рис. 5.13

Пример. На вертикально поставленный винт надета гайка (рис. 5.13). Ей сообщена угловая скорость 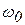такого направления, что гайка начинает подниматься. На какую высоту поднимется гайка до остановки? Трение отсутствует.

Решение. Пусть высота подъема гайки Н, тогда работа, совершаемая весом гайки, 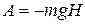. При движении гайка поднимается вдоль оси z вверх и вращается вокруг этой оси до остановки, следовательно, кинетическую энергию записать так

,

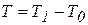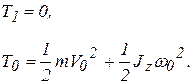(а)

Вычислим скорость движения гайки по оси z вверх V₀ и момент инерции гайки относительно этой оси J_z.

Пусть V₀ скорость движения гайки вдоль оси винта в начале движения. Она найдется из пропорции

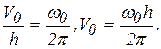(б)

Примем, что гайка имеет форму цилиндра с осевым отверстием радиусом r. Если m масса гайки, то ее момент инерции относительно винта будет определяться следующим образом:

,

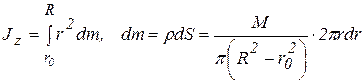где - плотность.

Тогда

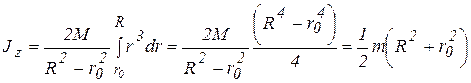. (в)

Кинетическая энергия (а) с учетом (б) и (в) запишем

.

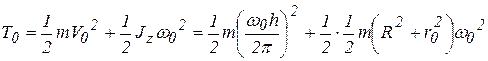Теорема об изменении кинетической энергии, имеем

Т₁-Т₀ = А,

или

,

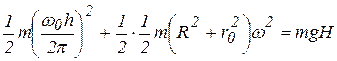откуда

.

<2 3 4 5 6 78>

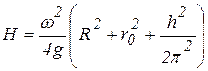Дата добавления: 2019-12-09; просмотров: 483;