Кинетическая энергия системы. Теорема Кенига

Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. 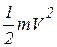. Кинетическая энергия, является скалярной положительной величиной. В системе СИ, единицей измерения кинетической энергии является джоуль: .

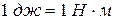Кинетической энергией механической системы называется сумма кинетических энергий всех точек, входящих в систему:

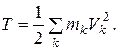(5.11)

Скорости 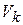точек системы (5.1) определяются относительно неподвижной системы отсчета.

Совместим начало координат 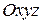с центром масс системы. Предположим, что механическая система вместе с системой координат 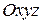движется поступательно относительно неподвижной системы координат 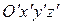(рис.5.7). Точка 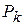– точка системы.

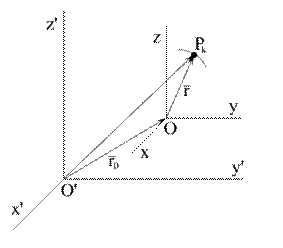Рис. 5.7

Тогда, на основании теоремы о сложении скоростей, абсолютная скорость точки Р_k. системы запишется так векторная сумма переносной и относительной скоростей:

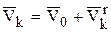, (а)

где 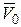– скорость начала подвижной системы координат (переносная скорость, т.е. скорость центра масс системы); 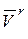– скорость точки Р_k относительно подвижной системы координат Охуz (относительная скорость).

Подставляя (а) в формулу (5.11), получаем

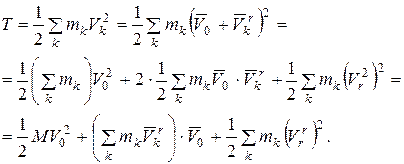(5.12)

Здесь 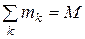- масса всей системы.

Радиус-вектор центра масс системы в подвижной системе координат определяется, согласно (2.1), – 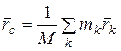, откуда 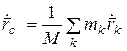, т.е. 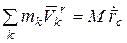. Поскольку начало координат О является центром масс системы, то 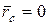, тогда 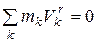, т.е. вторая сумма в выражении (5.12) равна нулю.

Таким образом, кинетическая энергия системы (5.12) имеет вид

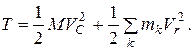(5.13)

Это равенство определяет теорему Кенига.

Теорема. Кинетическая энергия системы равна сумме кинетической энергии, которую имела бы материальная точка, расположенная в центре масс системы и имеющая массу, равную массе системы, и кинетической энергии движения системы относительно центра масс.