Теорема об изменении кинетической энергии системы
Пусть точки системы массой 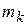 переместились так, что их радиус-векторы
переместились так, что их радиус-векторы 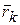 в инерциальной системе отсчета получили приращение
в инерциальной системе отсчета получили приращение 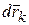 . Найдем, как при этом изменилась кинетическая энергия Т системы.
. Найдем, как при этом изменилась кинетическая энергия Т системы.
Согласно (5.11), кинетическая энергия системы
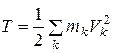 .
.
Вычислим дифференциал кинетической энергии системы и преобразуем полученное выражение
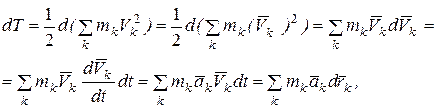
здесь 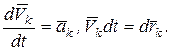
Принимая во внимание, что 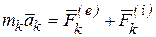 , где
, где 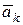 - ускорение точки а
- ускорение точки а 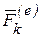 и
и 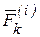 - равнодействующие внешних и внутренних сил, приложенных к точке, перепишем последнее равенство в виде
- равнодействующие внешних и внутренних сил, приложенных к точке, перепишем последнее равенство в виде
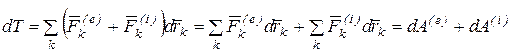 .
.
Таким образом,
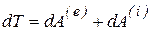 . (5.23)
. (5.23)
Последнее равенство выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме: дифференциал кинетической энергии системы равен элементарной работе всех сил системы.
Частный случай. Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:
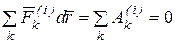 .
.
Следовательно, теорему об изменении кинетической энергии (5.23) для твердого тела можно записать в виде
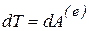 . (5.24)
. (5.24)
Изменение кинетической энергии твердого тела при каком-либо элементарном перемещении равно элементарной работе внешних сил, действующих на тело.
Если обе части (5.24) проинтегрировать между двумя положениями – начальным и конечным, в которых соответственно кинетическая энергия 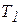 и
и 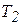 , получаем
, получаем
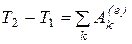 . (5.25)
. (5.25)
Пример 1. Диск массой m=5 кг и радиусом 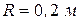 приводится в движение постоянной силой
приводится в движение постоянной силой 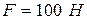 , приложенной в точке А (рис. 5.6). Диск катится по шероховатой поверхности вправо без скольжения. Определить скорость центра масс С катушки в момент, когда он переместится на расстояние
, приложенной в точке А (рис. 5.6). Диск катится по шероховатой поверхности вправо без скольжения. Определить скорость центра масс С катушки в момент, когда он переместится на расстояние 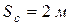 , коэффициент трения скольжения
, коэффициент трения скольжения 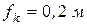 ,
, 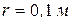 , радиус инерции диска
, радиус инерции диска 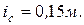
Решение. Диск совершает плоское движение. Запишем теорему об изменении кинетической энергии для твердого тела
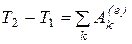 . (а)
. (а)
Вычислим кинетическую энергию диска. В начальный момент времени диск находился в покое, т.е. 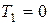 . Кинетическая энергия в конечном положении диска
. Кинетическая энергия в конечном положении диска
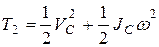 ,
,
где 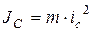 ,
, 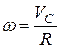 , следовательно,
, следовательно,
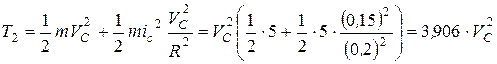 .
.
Работа внешних сил на перемещении центра масс 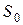 была вычислена на стр 91:
была вычислена на стр 91:
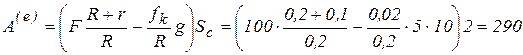 .
.
Находим искомую скорость центра масс диска. Имеем
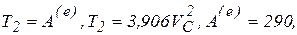
следовательно,
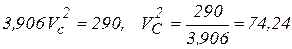 , откуда. VC=8,62 м/с.
, откуда. VC=8,62 м/с.
Пример 2. Механическая система (рис. 5.12) состоит из составного диска 1 (m1g=40H, R1=0,4м, r1=0,2м, радиус инерции относительно оси вращения i1=0,3м), обмотанного нерастяжимыми нитями, на концах которых прикреплен груз 2 (m2g=60H) и однородный каток 3 (m3g=20H). Каток катится без скольжения по наклонной шероховатой поверхности с углом наклона 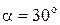 . К диску приложена пара сил, с моментом М=80H·м, а к оси катка сила F=800H.
. К диску приложена пара сил, с моментом М=80H·м, а к оси катка сила F=800H.
Вычислить ускорение, с которым будет опускаться груз 2.
Решение. Вычислим кинетическую энергию системы, равную сумме энергией всех ее тел
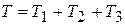 . (а)
. (а)
Диск (тело 1) вращается вокруг центра вращения О, груз (тело 2) движется поступательно, а каток (тело 3) – плоскопараллельно, тогда кинетическая энергия каждого тела механической системы, соответственно, имеет вид
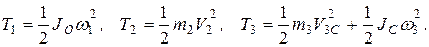 (б)
(б)
Моменты инерции диска и катка вычисляются по формулам
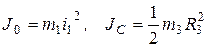 . (в)
. (в)
Выразим линейные и угловые скорости в выражении (б) через перемещение второго груза S и его скорость 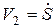 . Направления движений тел изображены на рис. 5.12.
. Направления движений тел изображены на рис. 5.12. 
Имеем: 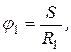 тогда
тогда 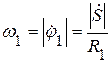 ;
;
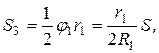 тогда
тогда  ; (г)
; (г)
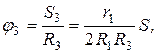 тогда
тогда 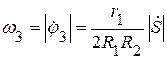 .
.
Здесь учтено, что расстояния, пройденные точками А, В и С, связаны между собой следующим образом: 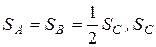 ≡
≡ 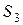 .
.
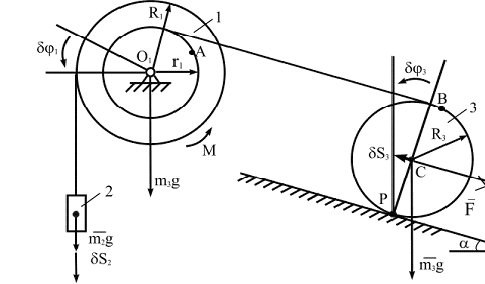
Рис. 5.12
Подставляя выражения (г) и (в) в (б), получим
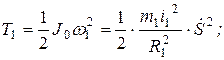
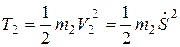 ;
; 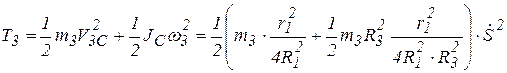 .
.
Кинетическая энергия системы равна сумме кинетических энергий элементов системы, т.е.
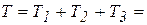
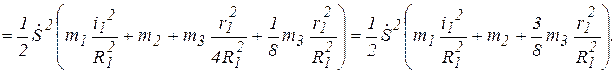
Выражение, стоящее в скобках имеет размерность массы (кг), следовательно, слагаемые в скобке представляют собой приведенную массу заданной механической системы, обозначим ее 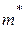 , тогда кинетическая энергия системы примет вид
, тогда кинетическая энергия системы примет вид
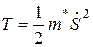 .
.
Вычислим значение приведенной массы системы
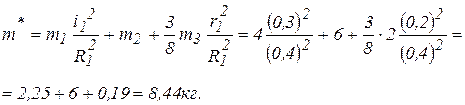
Вычислим работу, совершенную внешними силами, сообщив механической системе перемещение при котором груз 2 опустится на δS. Тогда, имея в виду (г), получим
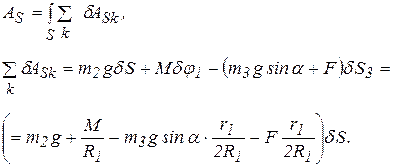
Выражение, стоящее в скобках имеет размерность силы (н), следовательно, слагаемые в скобке представляют собой приведенную силу заданной механической системы, обозначим ее 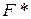 , тогда
, тогда
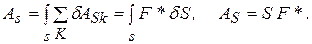
Вычислим значение приведенной силы заданной системы
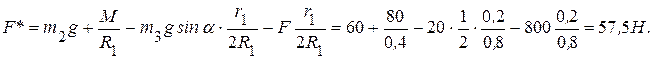
Запишем теорему (5.25)
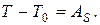
В начальный момент времени система находилась в покое, следовательно, 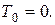 Имеем
Имеем
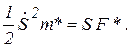 (д)
(д)
Продифференцировав по времени правую и левую части уравнения (д), получим
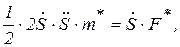 откуда
откуда 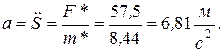
Дата добавления: 2019-12-09; просмотров: 1023;











