Теорема об изменении кинетической энергии. Работа силы
Пусть сила 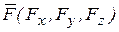 – равнодействующая всех сил системы, приложена к точке Р, а
– равнодействующая всех сил системы, приложена к точке Р, а 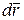 (dx, dy, dz) – элементарное перемещение точки Р вдоль ее траектории Р1 Р2 (рис. 5.1). Элементарной работой dА силы
(dx, dy, dz) – элементарное перемещение точки Р вдоль ее траектории Р1 Р2 (рис. 5.1). Элементарной работой dА силы 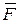 называют скалярное произведение
называют скалярное произведение
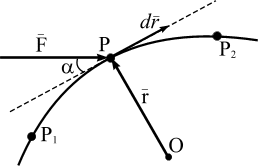 Рис.5.1
Рис.5.1
|
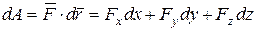 . (5.1)
. (5.1)
Элементарная работа является скалярной величиной. Если 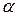 - угол между силой
- угол между силой 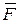 и направлением перемещения
и направлением перемещения 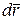 , то выражение (5.1) можно представить в виде
, то выражение (5.1) можно представить в виде
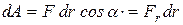 , (5.2)
, (5.2)
где 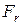 - проекция силы
- проекция силы 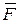 на направление элементарного перемещения (или направление скорости точки).
на направление элементарного перемещения (или направление скорости точки).
Знак элементарной работы зависит от знака функции 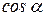 . Если
. Если 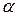 - острый угол, то
- острый угол, то 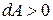 , если
, если 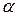 - тупой угол, то
- тупой угол, то 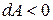 , если
, если 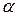
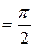 , то
, то 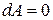 .
.
Пусть точка Р совершает конечное перемещение из положения 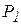 в положение
в положение 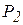 , описывая дугу
, описывая дугу 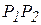 . Разобьем дугу на n произвольных малых участков, обозначив длину участка с номером k через
. Разобьем дугу на n произвольных малых участков, обозначив длину участка с номером k через 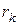 . Тогда элементарная работа силы на k-м участке будет равна
. Тогда элементарная работа силы на k-м участке будет равна 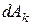 , а на всем пути от
, а на всем пути от 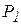 до
до 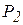 - сумме работ на отдельных участках
- сумме работ на отдельных участках
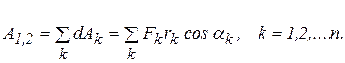
Точное значение работы получим, переходя к пределу, при условии, что число участков n неограниченно возрастает, а длина каждого участка 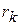 убывает:
убывает:
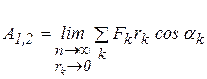 .
.
Такой предел называется криволинейным интегралом первого рода по дуге 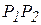 и записывается следующим образом
и записывается следующим образом
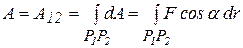 . (5.3)
. (5.3)
Результат интегрирования является полной работой А силы F на рассматриваемом конечном перемещении вдоль пути 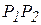 .
.
Дата добавления: 2019-12-09; просмотров: 708;











