Дискретные случайные величины
Случайные величины принято обозначать заглавными буквами латинского алфавита:
X, Y, Z, …, а их возможные значения – соответствующими малыми буквами: x, y, z, …
Пример 6) Два стрелка стреляют по мишени. Первый попадает в мишень с вероятностью 0,6 (дает 60% попаданий), второй – с вероятностью 0,7 (70% попаданий). Рассмотрим случайную величину Х со значениями, соответствующими возможному количеству попаданий в мишень при одновременном залпе обоих стрелков. У случайной величины Х три возможных значения:
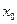 - ни одного попадания в мишень,
- ни одного попадания в мишень,
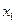 - одно попадание и
- одно попадание и
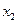 - два попадания.
- два попадания.
Для подсчета вероятностей указанных исходов, введем обозначения событий:
А = {первый стрелок поразил мишень},
В = {второй стрелок поразил мишень}.
Очевидно, Р(А)=0,6, Р(В)=0,7. Тогда применяя теоремы сложения и умножения вероятностей:
Р( 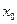 )=Р(
)=Р( 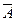 )´Р(
)´Р( 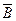 )=(1-0,6)´(1-0,7)=0,4´0,3=0,12.
)=(1-0,6)´(1-0,7)=0,4´0,3=0,12.
Р( 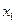 )=Р(
)=Р( 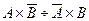 )=Р(А)´Р(
)=Р(А)´Р( 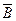 )+Р(
)+Р( 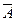 )´Р(В)=0,6´0,3+0,4´0,7=0,46.
)´Р(В)=0,6´0,3+0,4´0,7=0,46.
Р( 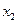 )=Р(А´В)=Р(А)´Р(В)=0,6´0,7=0,42.
)=Р(А´В)=Р(А)´Р(В)=0,6´0,7=0,42.
Ñ Составим таблицу соответствия, устанавливающую связь между возможными значениями случайной величины и их вероятностями, которая называется законом распределения соответствующей дискретной случайной величины.
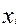
| 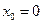
| 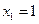
| 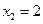
|
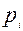
| 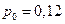
| 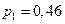
| 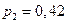
|
Как видим 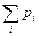 =
= 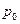 +
+ 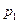 +
+ 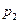 =0,12+0,46+0,42=1
=0,12+0,46+0,42=1
(так как возможные исходы 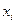 составляют полную группу).
составляют полную группу).
Ñ График, соответствующий заданному закону распределения, называется многоугольником распределения случайной величины.
Для данного примера 6, многоугольник распределения имеет вид:
 | |||
 |
0,5
1 2 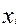
Дата добавления: 2016-06-05; просмотров: 1849;











