Математическое ожидание случайного процесса и его свойств
Математическим ожиданием случайного процесса (СП) X(t) называется неслучайная функция mx(t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайного процесса mx(t) = M[X(t)].
Если сечение случайного процесса X(t) при заданном t представляет собой дискретную случайную величину с законом распределения:
| X(t) | x1(t) | x2(t) | … | xn(t) |
| pi | p1(t) | p2(t) | … | pn(t) |
то его математическое ожидание вычисляется по формуле: mx(t) = 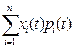 .
.
В случае, если сечение СП X(t) при данном t – непрерывная случайная величина с плотностью f(t, x) , то его математическое ожидание вычисляется по формуле:
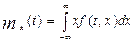 .
.
Свойства математического ожидания СП:
1) Для неслучайной функции 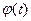 ,
, 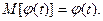
2) Неслучайный множитель 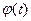 можно выносить за знак математического ожидания:
можно выносить за знак математического ожидания: 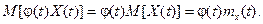
3) Математическое ожидание суммы двух случайных функций равно сумме их математических ожиданий: 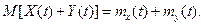
4) Математическое ожидание суммы случайной и неслучайной функций равно сумме их математических ожиданий: 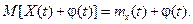
Дата добавления: 2016-06-05; просмотров: 5115;











