Пример стохастической модели роста популяции

Рассмотрим стохастический аналог упрощенного процесса роста популяции с учетом только размножения.

При детерминистском подходе предполагается, что существует определенная скорость размножения 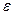, такая, что численность популяции n за время 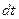увеличивается на 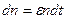. Принимая 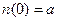и деля обе части на 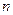, после приравнивания интегралов обеих частей равенства, 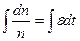, получим: .

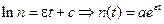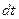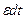При построении вероятностной модели, можно принять простейшее предположение о том, что вероятность появления одного потомка у данной особи в интервале времени равна . Тогда вероятность появления одной новой особи в целой популяции за время 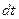равна .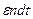

Обозначим 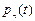- вероятность того, что в момент t в популяции имеется ровно n особей. Тогда то, что в момент 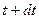число особей в популяции равно 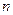, означает, что либо: а) в момент t было n особей и за время 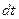это число не изменилось, либо: б) в момент 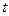было 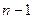особей и за время 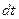появилась еще одна.

Получаем соотношение: 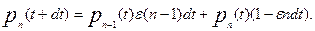Откуда после перегруппировки и деления на 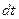получим:

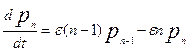(1)

Это уравнение справедливо при 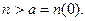Легко доказать, что при 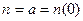уравнение упрощается и имеет вид:

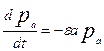(2)

Так как в случае, когда процесс начинается при значении 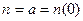, отсутствует член, содержащий .

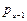Уравнение (2) легко интегрируется с учетом того, что 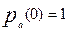(аналогия с детерминистской моделью). Умножая обе части (2) на 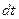, деля на 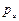и приравнивая интегралы обеих частей, получим:

= .

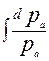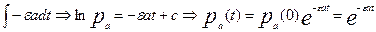Полученный результат подставляем в уравнение (1) для 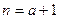и интегрируем, используя начальное условие 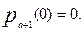Решая соответствующее линейное неоднородное уравнение первого порядка, получим:

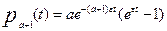(3)

Формула (3) подставляется далее в уравнение (1) для 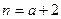и решается полученное уравнение с начальным условием 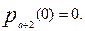Повторяя далее процесс, придем к решению в общем виде:

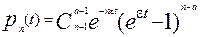
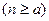(4)

То есть пришли к частному случаю биномиального распределения.