Формула полной вероятности
Пусть 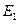 ,
, 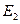 , …
, … 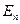 образуют полную группу событий. Для некоторого случайного события A можно представить:
образуют полную группу событий. Для некоторого случайного события A можно представить:
A=A´ 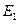 +A´
+A´ 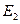 + … +A´
+ … +A´ 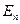
Откуда: Р(A)= 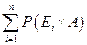 =
= 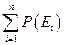 ´
´ 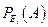
(в силу несовместимости событий A´ 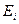 ).
).
· Детали изготавливают на двух станках. Производительность первого в два раза больше, чем второго. Первый станок дает 5% бракованных деталей (95% - качественных), второй – 10% брака (90% - качественных). Сколько процентов качественных деталей изготавливают за смену на обоих станках?
Обозначим: E1={деталь изготовлена на 1 станке},
E2={деталь изготовлена на 2 станке},
A ={произвольно взятая деталь - стандартна}.
Здесь: Р( 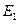 )=
)= 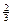 , Р(
, Р( 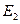 )=
)= 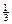 ,
, 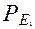 (A)=0,95,
(A)=0,95, 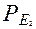 (A)=0,9
(A)=0,9
По формуле полной вероятности (для двух гипотез 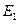 и
и 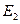 ):
):
Р(A)=Р( 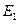 )´
)´ 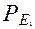 (A) + Р(
(A) + Р( 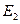 )´
)´ 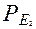 (A) =
(A) = 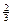 ´0,95+
´0,95+ 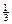 ´0,9»0,93.
´0,9»0,93.
Вывод: Примерно 93% изготавливаемых за смену деталей (при одновременной работе обоих станков) - качественные.
Формула Байеса
Представляет собой, в определенном смысле, решение обратной задачи.
Так, в предыдущем примере можно задаться вопросом:
Какой процент из всех качественных деталей, изготовленных за смену, приходится на первый станок (соответственно, второй)?
Формула Байеса выводится из формулы полной вероятности, если для каждого слагаемого, в силу симметрии (А´ 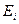 =
= 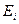 ´А), представить: Р(
´А), представить: Р( 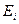 )´
)´ 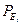 (А)=Р(А)´
(А)=Р(А)´ 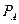 (
( 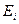 ).
).
Откуда: 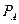 (
( 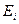 ) =
) = 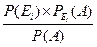 =
= 
· Отвечая на поставленный вопрос, получим:
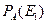 =
= 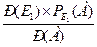 =
= 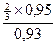 »0,68 (68%)
»0,68 (68%)
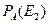 =
= 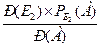 =
= 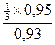 »0,32 (32%)
»0,32 (32%)
Вывод: Из всех качественных деталей, изготовленных за смену, 68% приходится на первый станок и 32% - на второй станок.
Дата добавления: 2016-06-05; просмотров: 1614;











