Непрерывные случайные величины
Для непрерывной случайной величины, в отличие от дискретной, нельзя составить закон распределения. Поэтому для таких величин оценивают вероятность попадания в заданный интервал.
Введем функцию аргумента Х:
F(X) = P(X<x)
Интегральной функцией распределения случайной величины Х называется вероятность события, состоящего в том, что случайная величина Х примет значение, меньшее заданного числа (аргумента) х.
Будем предполагать, что функция F(X) – непрерывна.
Свойства интегральной функции распределения:
1) 0£F(X)£1
2) F(X) – неубывающая функция, т.е. если 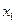 <
< 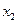 , то F
, то F 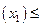 F
F 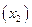 .
.
3) F(-¥)=0, F(+¥)=1
(Cвойства 1-3 следуют из определения вероятности).
4) Р(a<Х<b) = F(b) – F(a)
- Так как событие {X<b} эквивалентно событиям {X<a} или {a£Х<b}, то по теореме сложения вероятностей:
P(X<b)=P(X<a)+P(a£X<b)=P(X<a)+P(X=a)+P(a<X<b)
Из непрерывности F(X) легко доказать, что Р(Х=a)=0 (принимая, в частности, b=a+Dх и Dх®0). Откуда:
Р(a<Х<b)=Р(Х<b)-Р(Х<a) = F(b)-F(a)
Ñ Дифференциальной функцией распределения непрерывной случайной величины Х (или ее плотностью вероятности) называется функция j(X), равная производной ее интегральной функции: j(X) = 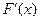
Дата добавления: 2016-06-05; просмотров: 1643;











