Свойства математического ожидания дискретной случайной величины

1) Математическое ожидание постоянной случайной величины равно этой величине:

М(С) = С

2) Постоянный множитель можно выносить за знак математического ожидания:

М(С´Х)= С´М(Х)

3) Если X, Y – две дискретные случайные величины, то:

а) M(X+Y) = M(X) + M(Y)

b) M(X-Y) = M(X) - M(Y)

c) M(X´Y) = M(X) ´ M(Y) (если X, Y- независимы).

Все свойства примем без доказательства.

Ñ Дисперсией случайной величины Х называется среднее значение квадрата отклонения с.в. от ее математического ожидания.

Обозначается: D(X) = M = ´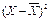

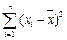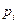
Подсчитаем значение дисперсии (мера рассеяния или «разброса» значений с.в. относительно среднего) для примера 6:

D(X) =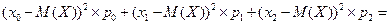

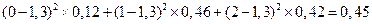
Свойства дисперсии дискретной случайной величины

1) Дисперсия постоянной с.в. С равна нулю.

D(C) = 0

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(C´X) = 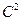´D(X)

3) Если X,Y – независимые случайные величины, то:

D(X±Y) = D(X) + D(Y)

4) D(X) = M( ) -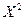

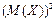
Ñ Средним квадратическим отклонением s(Х) случайной величины Х называется корень квадратный из ее дисперсии:

s(Х) = ÖD(X)

Так, для примера 6, s(Х) = Ö0,45 » 0,67.