Вероятность попадания нормально распределенной случайной величины в заданный интервал.

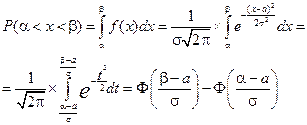
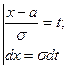
Где 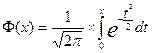- интегральная функция Лапласа, задается таблично.

Из свойств определенного интеграла Ф(-х)= - Ф(х), т.е. функция Ф(х) – нечетная.

Отсюда выводятся следующие (производные) формулы:

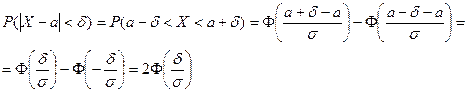
Полагая: а) d=s

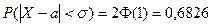(68%)

б) d=2s

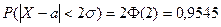(95%)

в) d=3s

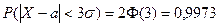(»100%)

Правило трех сигм (3s):практически достоверно, что при однократном испытании, отклонение нормально распределенной случайной величины от ее математического ожидания не превышает утроенного средне-квадратического отклонения.

Задача: Предполагается, что масса вылавливаемых в пруду зеркальных карпов есть случайная величина Х, имеющая нормальное распределение с математическим ожиданием a=375 г. и средним квадратическим отклонением s = 25 г. Требуется определить:

А) Вероятность, что масса случайно выловленного карпа окажется не менее a=300 г. и не более b=425 г.

Б) Вероятность, что отклонение указанной массы от среднего значения (математического ожидания) по абсолютной величине будет меньше d= 40 г.

В) По правилу трех сигм найти минимальную и максимальную границы предполагаемой массы зеркальных карпов.

Решение:

А)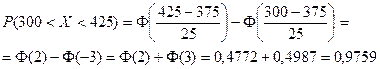

Вывод: Примерно 98% карпов, плавающих в пруду, имеют массу не менее 300 г. и не более 425 г.

Б)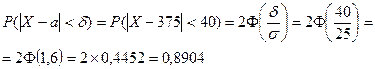

Вывод: Примерно 89% имеют массу от a-d = 375- 40 = 335 г. до a+d = 375 + 40 = 415 г.

В) По правилу трех сигм:

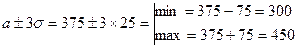
Вывод: Масса практически всех карпов (примерно 100%) заключена в интервале от 300 до 450 грамм.