Теорема об изменении кинетического момента

Пусть 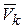- скорость точки массой 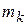системы в инерциальной системе отсчета, а 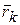- ее радиус-вектор относительно начала координат (рис. 3.11). Кинетический момент системы относительно начала координат вычисляется по формуле

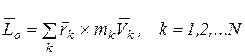. (3.17)

Продифференцировав по времени обе части равенства (3.17), получим

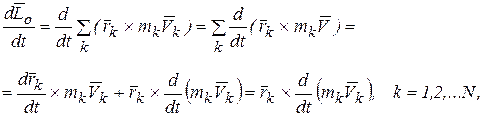(3.17а)

поскольку 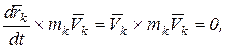т.к. .

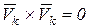Если к k-ой точке системы приложить внешние и внутренние силы, то, согласно (3.3), получим

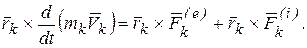
Суммируем правые и левые части последнего соотношения по всем точкам системы

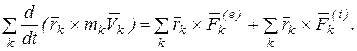(а)

Второе слагаемое полученного равенства, согласно (3.2), равно нулю. Подставляя (а) в (3.17а), получим

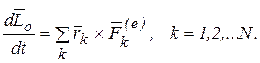
Правая часть в этом равенстве равна главному моменту 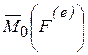внешних сил относительно центра О.

Таким образом,

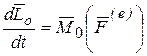. (3.18)

Равенство (3.18) представляет собой теорему об изменении кинетического момента относительно неподвижного центра: производная по времени от кинетического момента системы относительно неподвижного центра равна главному моменту внешних сил системы относительно этого центра.

Проецируя (3.18) на прямоугольные оси координат, получаем

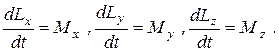(3.18,а)

Теорема об изменении кинетического момента позволяет изучать вращательное движение системы вокруг неподвижной оси.