Закон сохранения движения центра масс

Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. 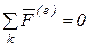, то из (3.6) следует, что ускорение центра масс 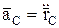равно нулю, следовательно, скорость центра масс 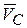является постоянной по модулю и направлению. Если, в частности, в начальный момент центр масс находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.

Из этой теоремы вытекает несколько следствий.

· Одними внутренними силами нельзя изменить характер движения центра масс системы.

· Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс находится в покое или движется равномерно и прямолинейно.

· Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.

· Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может вызвать только вращение тела вокруг центра масс).

Рассмотрим пример, иллюстрирующий закон сохранения движения центра масс.

Рис. 3.5

Пример 3. Два груза массам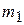и и 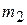соединены нерастяжимой нитью, переброшенной через блок (рис. 3.5), закрепленный на клине массой М. Клин опирается на гладкую горизонтальную плоскость. В начальный момент система находилась в покое. Найти перемещение клина по плоскости при опускании первого груза на высоту Н. Массой блока и нити пренебречь.

Решение. Внешними силами, действующими на клин вместе с грузами, являются силы тяжести , 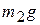и Mg, а также нормальная реакция гладкой горизонтальной поверхности N. Следовательно,

.

Поскольку в начальный момент система находилась в покое, имеем .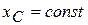

Вычислим координату центра масс системы при и в момент t₁, когда груз весом 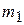g опустится на высоту H.

Для момента :

,

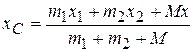где 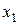, , х – соответственно координаты центра масс грузов весом 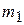g, 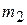g и клина весом Мg.

Предположим, что клин в момент времени 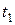переместится в положительном направлении оси Ox на величину L, если груз весом 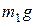опустится на высоту Н. Тогда, для момента

,

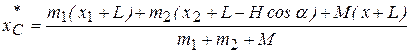т.к. грузы вместе с клином передвинутся на L вправо, a груз 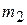переместится на расстояние 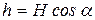по клину вверх. Так как 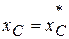, то после вычислений получим

,

откуда .