Законы сохранения количества движения

Законы сохранения получаются как частные случаи теоремы об изменении количества движения. Возможны два частных случая.

· Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т.е. 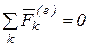, то из теоремы следует (3.9), что

,

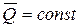т.е. если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению.

· Если проекция главного вектора внешних сил на какую-либо координатную ось равна нулю, например Ох, т.е. , то проекция количества движения на эту ось величина постоянная

.

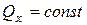Рассмотрим пример применения закона сохранения количества движения.

Пример 5. Баллистический маятник представляет собой тело массой 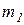, подвешенное на длинной нити (рис. 3.8, а).

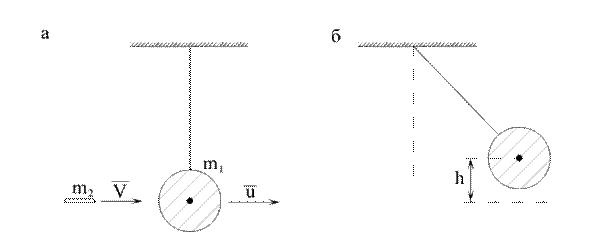
Рис. 3.8

Пуля массой 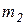, движущаяся со скоростью V и попадающая в неподвижное тело, застревает в нем, и тело отклоняется. Какова была скорость пули, если тело поднялось на высоту h (рис. 3.8 б)?

Решение. Пусть тело с застрявшей пулей приобрело скорость 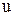. Тогда, пользуясь законом сохранения количества движения при взаимодействии двух тел, можно записать

.

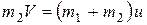Скорость 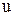можно вычислить, воспользовавшись законом сохранения механической энергии 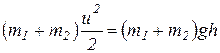. Тогда 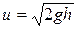. В результате находим

.

Пример 6. Вода входит в неподвижный канал (рис. 3.9) переменного сечения со скоростью 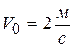под углом 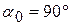к горизонту; площадь поперечного сечения канала при входе 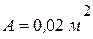; скорость воды у выхода из канала 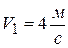и составляет угол 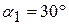с горизонтом.

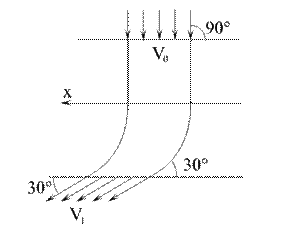Определить горизонтальную составляющую реакции, которую вода оказывает на стенки канала. Плотность воды 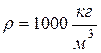. Рис.3.9

Решение. Будем определять горизонтальную составляющую реакции, оказываемой стенками канала на воду. Эта сила равна по модулю и противоположна по знаку искомой силе. Имеем, согласно (3.11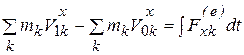а),

. (а)

Здесь .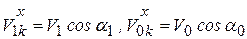

Вычисляем массу объема жидкости, поступающей в канал за время t:

,

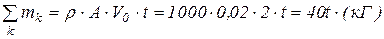т.е.

(б)

Величина rАV₀ называется секундной массой - масса жидкости, протекающей через любое сечение трубы в единицу времени.

Такое же количество воды покидает канал за это же время. Начальная и конечная скорости даны в условии.

Вычислим правую часть равенства (а) которая определяет сумму проекций на горизонтальную ось внешних сил, приложенных к системе (воде). Единственной горизонтальной силой является горизонтальная составляющая равнодействующей реакции стенок R_x. Эта сила при установившемся движении воды является постоянной. Поэтому

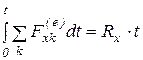. (в)