Закон сохранения кинетического момента
Если главный момент внешних сил относительно центра 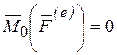 , то из (3.18) следует закон сохранения кинетического момента:
, то из (3.18) следует закон сохранения кинетического момента:
Если главный момент внешних сил относительно центра 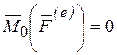 , то кинетический момент системы относительно того же центра постоянен по модулю и направлению, т.е.:
, то кинетический момент системы относительно того же центра постоянен по модулю и направлению, т.е.:
 (3.21)
(3.21)
Если  ,
,  ,
, 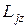 - проекции вектора
- проекции вектора 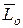 на соответствующие оси координат, то из (3.21) следует три первых интеграла
на соответствующие оси координат, то из (3.21) следует три первых интеграла
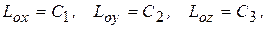
где 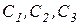 - произвольные постоянные.
- произвольные постоянные.
Закон сохранения кинетического момента системы показывает, что одни внутренние силы не могут изменить кинетический момент системы, так же, как они не изменяют ее количество движения.
Для тела, вращающегося относительно неподвижной главной оси z, имеем
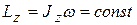 ,
,
или
 , (3.22)
, (3.22)
где 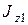 и
и 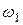 - момент инерции тела и его угловая скорость относительно оси вращения в произвольный момент времени
- момент инерции тела и его угловая скорость относительно оси вращения в произвольный момент времени 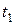 ;
; 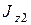 и
и 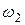 - момент инерции тела угловая скорость в момент времени
- момент инерции тела угловая скорость в момент времени 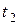 .
.
Закон сохранения кинетического момента в виде (3.22) используют в своей работе фигуристы, акробаты, танцоры.
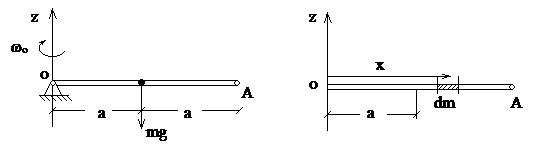
Пример 7. Горизонтальная трубка ОА весом Mg и длиной 2а вместе с шариком, находящимся в ней на расстоянии 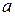 от конца О и привязанным нитью к этому концу (рис. 3.12а), сначала вращается по инерции вокруг вертикальной оси z, проходящей через центр О, с постоянной угловой скоростью w0, затем нить перерезают. Определить угловую скорость вращения трубки в тот момент, когда шарик вылетает из нее, если вес шарика равен mg.
от конца О и привязанным нитью к этому концу (рис. 3.12а), сначала вращается по инерции вокруг вертикальной оси z, проходящей через центр О, с постоянной угловой скоростью w0, затем нить перерезают. Определить угловую скорость вращения трубки в тот момент, когда шарик вылетает из нее, если вес шарика равен mg.
а б
Рис.3.12
Решение. Связи допускают поворот всей системы, состоящей из трубки и шарика, вокруг неподвижной вертикальной оси oz. Внешние силы Mg и mg параллельны оси вращения oz, следовательно, момент внешних сил относительно оси вращения равен нулю.
Момент инерции трубки обозначим через 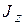 и вычислим его (рис. 3.12,б). По определению
и вычислим его (рис. 3.12,б). По определению 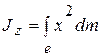 , где dm=rdx,
, где dm=rdx,  -плотность трубки. Тогда
-плотность трубки. Тогда  .
.
Момент инерции шарика относительно оси oz до отрыва нити равен ma2, а после отрыва нити в момент вылета шарика из трубки равен m(2a)2=4ma2.
Запишем закон сохранения кинетического момента (3.22)

откуда
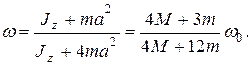
Дата добавления: 2019-12-09; просмотров: 638;











