Теорема об изменении количества движения системы
Пусть к точкам системы приложены внешние и внутренние силы. Тогда для каждой точки системы можно применить дифференциальные законы движения (3.3), имея в виду, что 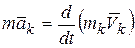 :
:
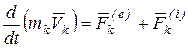 .
.
Суммируя по всем точкам системы, получим
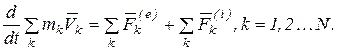
По свойству внутренних сил 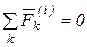 и по определению
и по определению 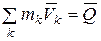 имеем
имеем
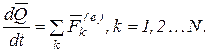 (3.9)
(3.9)
Умножая обе части этого уравнения на dt, получим теорему об изменении количества движения в дифференциальной форме:
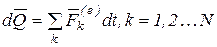 , (3.10)
, (3.10)
т.е. дифференциал количества движения механической системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на точки механической системы.
Вычисляя интеграл от обеих частей (3.10) по времени от 0 до t, получим теорему в конечной или интегральной форме
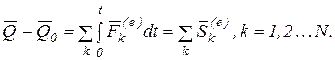 (3.11)
(3.11)
В проекциях на координатные оси будем иметь
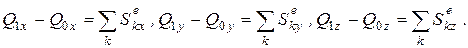 (3.11а)
(3.11а)
Изменение количества движения механической системы за время t, равно векторной сумме всех импульсов внешних сил, действующих на точки механической системы за то же время.
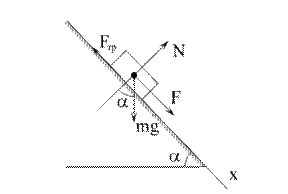 Рис. 3.7
Рис. 3.7
|
Пример 4. Груз массой m спускается вниз по наклонной плоскости из состояния покоя под действием силы F, пропорциональной времени: 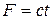 , где
, где 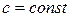 (рис. 3.7). Какую скорость приобретет тело через t секунд после начала движения, если коэффициент трения скольжения груза о наклонную плоскость равен f.
(рис. 3.7). Какую скорость приобретет тело через t секунд после начала движения, если коэффициент трения скольжения груза о наклонную плоскость равен f.
Решение. Изобразим силы, приложенные к грузу: mg – сила тяжести груза, N – нормальная реакция плоскости, 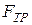 - сила трения скольжения груза о плоскость, причем
- сила трения скольжения груза о плоскость, причем 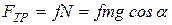 . Направление всех сил изображено на рис. 3.7.
. Направление всех сил изображено на рис. 3.7.
Направим ось х вдоль наклонной плоскости вниз. Запишем теорему об изменении количества движения (3.11) в проекции на ось х:
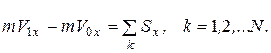 (а)
(а)
По условию 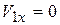 , т.к. в начальный момент времени груз находился в состоянии покоя. Сумма проекций импульсов всех сил на ось х равна
, т.к. в начальный момент времени груз находился в состоянии покоя. Сумма проекций импульсов всех сил на ось х равна
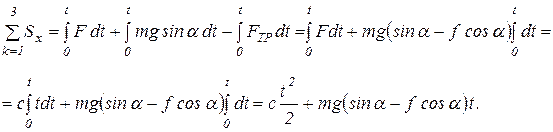
Следовательно,
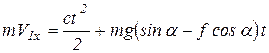 ,
,
откуда
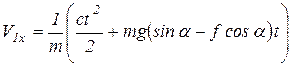 .
.
Дата добавления: 2019-12-09; просмотров: 553;











