Подставляя (б) и (в) в (а), получаем

,

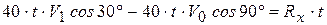Откуда

.

Кинетический момент системы

Главный момент количества движения системы

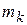Пусть - радиус-вектор точки массой системы относительно некоторой точки А, называемой центром (рис. 3.10).

Рис. 3.10

Моментом количества движения (кинетическим моментом) точки 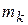относительно центра А называется вектор 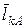, определяемый по формуле

. (3.12)

При этом вектор 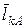направлен перпендикулярно плоскости, проходящей через центр А и вектор .

Моментом количества движения (кинетическим моментом) точки 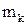относительно оси называется проекция на эту ось момента количества движения точки относительно любого выбранного на данной оси центра.

Главным моментом количества движения (кинетическим моментом) системы относительно центра А называется величина

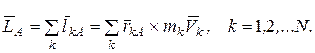(3.13)

Главным моментом количества движения (кинетическим моментом) системы относительно оси называется проекция на эту ось главного момента количества движения системы относительно любого выбранного на данной оси центра.