Бесконечные пределы

Пусть функция определена в некоторой правой окрестности точки и существует правосторонний предел функции 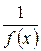, равный 0

.

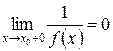Например, функция 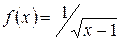определена пр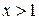и и .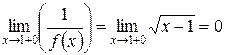

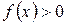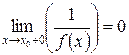Если в правой окрестности точки и , то говорят, что функция стремится к 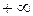при стремлении справа к точке и пишут

.

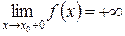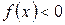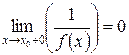Если в правой окрестности точки и , то говорят, что функция стремится к 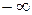при стремлении справа к точке и пишут

.

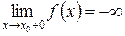Аналогично определяются бесконечные пределы слева в точке для функции , определенной в левой окрестности точки .

Пример. Для функции 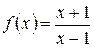найти пределы справа и слева в точке .

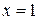Решение. Функция 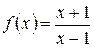определена в окрестности точки 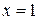, но не в самой этой точке, и .

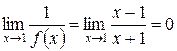Функция положительна правее точки 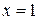и отрицательна левее точки 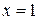, поэтому определению бесконечных пределов справа и слева получим

, .

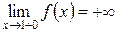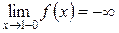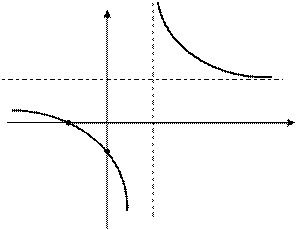
Учитывая, что 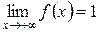, , 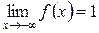получим искомый график.

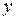
-1

-1

Если функция при , стремящемся к справа или слева, имеет бесконечный предел, то при графическом изображении этой функции проводим прямую 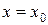. Это делает изображение более наглядным.