Пример 1. Сопоставление выборок по качественно определяемому признаку
В данном варианте использования критерия мы сравниваем процент испытуемых в одной выборке, характеризующихся каким-либо качеством, с процентом испытуемых в другой выборке, характеризующихся тем же качеством.
Допустим, нас интересует, различаются ли две группы студентов по успешности решения новой экспериментальной задачи. В первой группе из 20 человек с нею справились 12 человек, а во второй выборке из 25 человек – 10. В первом случае процентная доля решивших задачу составит 12/20 ∙ 100% = 60%, а во второй 10/25 ∙ 100% = 40%. Достоверно ли различаются эти процентные доли при данных n1 и n2?
Казалось бы, и «на глаз» можно определить, что 60% значительно выше 40%. Однако на самом деле эти различия при данных n1 и n2 недостоверны.
Проверим это. Поскольку нас интересует факт решения задачи, будем считать «эффектом» успех в решении экспериментальной задачи, а отсутствием эффекта – неудачу в ее решении.
Сформулируем гипотезы
H0: Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.
H1: Доля лиц, справившихся с задачей, в первой группе больше, чем во второй группе.
Теперь построим так называемую четырехклеточную, или четырехпольную, таблицу, которая фактически представляет собой таблицу эмпирических частот по двум значениям признака: «есть эффект» – «нет эффекта».
Таблица 14.1
Четырехклеточная таблица для расчета критерия при сопоставлении двух групп испытуемых, по процентной доле решивших задачу
| Группы | «Есть эффект», задача решена | «Нет эффекта», задача не решена | Суммы | ||||
| Количество испытуемых | % доля | Количество испытуемых | % доля | ||||
| 1 группа | (60%) | A | (40%) | Б | |||
| 2 группа | (40%) | В | (60%) | Г | |||
| Суммы |
В четырехклеточной таблице, как правило, сверху размечаются столбцы «Есть эффект» и «Нет эффекта», а слева – строки «1 группа» и «2 группа». Участвуют в сопоставлениях, собственно, только поля (ячейки) А и В, то есть процентные доли по столбцу «Есть эффект».
По таблице 18 приложения 1 определяем величины φ, соответствующие процентным долям в каждой из групп.
φ1(60%) = 1,772;
φ2(40%) = 1,369.
Теперь подсчитаем эмпирическое значение φ* по формуле:
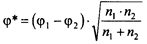 ,
,
где φ1 – угол, соответствующий большей % доле;
φ2 – угол, соответствующий меньшей % доле;
n1 – количество наблюдений в выборке 1;
n2 – количество наблюдений в выборке 2.
В данном случае:
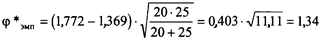 .
.
По таблице 19 приложения 1 определяем, какому уровню значимости соответствует φ*эмп = 1,34:
р = 0,09.
Можно установить и критические значения φ*, соответствующие принятым в психологии уровням статистической значимости:
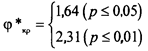 .
.
φэмп = 1,34
φэмп < φкр.
Построим «ось значимости».
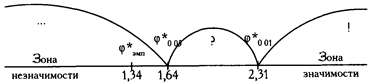
Полученное эмпирическое значение φ* находится в зоне незначимости.
Ответ: Н0 принимается. Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.
Можно лишь посочувствовать исследователю, который считает существенными различия в 20% и даже в 10%, не проверив их достоверность с помощью критерия φ*. В данном случае, например, достоверными были бы только различия не менее чем в 24,3%.
Похоже, что при сопоставлении двух выборок по какому-либо качественному признаку критерий φ может нас скорее огорчить, чем обрадовать. То, что казалось существенным, со статистической точки зрения может таковым не оказаться.
Гораздо больше возможностей порадовать исследователя появляется у критерия Фишера тогда, когда мы сопоставляем две выборки по количественно измеренным признакам и можем варьировать эффект.
Дата добавления: 2021-11-16; просмотров: 501;











