Сопоставление двух эмпирических распределений

<49 50 515253 54 55 >

Пример 13.13. Интересно сопоставить данные, полученные в предыдущем примере, с данными обследования X. Кларом 800 испытуемых (Klar. H, 1974.) X. Кларом было показано, что желтый цвет является единственным цветом, распределение которого по 8 позициям не отличается от равномерного. Для сопоставлений им использовался метод χ². Полученные им эмпирические частоты представлены в таблице 13.17.

Таблица 13.17

Эмпирические частоты попадания желтого цвета на каждую из 8 позиций в исследовании X. Клара (по: Klar H., 1974) (n = 800)

Разряды-позиции желтого цвета									Сумма
Эмпирические частоты

Сформулируем гипотезы

H₀: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке Х. Клара не различаются.

H₁: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара отличаются друг от друга.

Поскольку в данном случае мы будем сопоставлять накопленные эмпирические частости по каждому разряду, теоретические частости нас не интересуют.

Все расчеты будем проводить в таблице по алгоритму.

АЛГОРИТМ
расчета критерия λ при сопоставлении двух эмпирических

распределений

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты, полученные в распределении 1 (первый столбец) и в распределении 2 (второй столбец).

2. Подсчитать эмпирические частости по каждому разряду для распределения 1 по формуле:

f^*_э= f_э/n₁,

где f_э– эмпирическая частота в данном разряде;

n₁ – количество наблюдении в выборке.

Занести эмпирические частости распределения 1 в третий столбец.

3. Подсчитать эмпирические частости по каждому разряду для распределения 2 по формуле:

f^*_э= f_э/n₂,

где f_э – эмпирическая частота в данном разряде;

n₂ – количество наблюдений во 2-й выборке.

Занести эмпирические частости распределения 2 в четвертый столбец таблицы.

4. Подсчитать накопленные эмпирические частости для распределения 1 по формуле:

∑f^*_j = ∑f^*_j_-1+ f^*_j,

где ∑f^*_j_-1 – частость, накопленная на предыдущих разрядах;

j – порядковый номер разряда;

f^*_j_-1 – частость данного разряда.

Полученные результаты записать в пятый столбец.

5. Подсчитать накопленные эмпирические частости для распределения 2 по той же формуле и записать результат в шестой столбец.

6. Подсчитать разности между накопленными частостями по каждому разряду. Записать в седьмой столбец абсолютные величины разностей без их знака. Обозначить их как d.

7. Определить по седьмому столбцу наибольшую абсолютную величину разности d_max.

8. Подсчитать значение критерия λ по формуле:

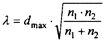где n₁– количество наблюдений в первой выборке;

n₂– количество наблюдении во второй выборке.

9. По таблице 17-Б приложения 1 определить, какому уровню статистической значимости соответствует полученное значение λ. Если λ_эмп≥ l,36, различия между распределениями достоверны.

Последовательность выборок может быть выбрана произвольно, так как расхождения между ними оцениваются по абсолютной величине разностей. В нашем случае первой будем считать отечественную выборку, второй – выборку Клара.

Таблица 13.18

Расчет критерия при сопоставлении эмпирических распределений желтого цвета в отечественной выборке (n₁= 102) и выборке Клара (n₂= 800)

Позиция желтого цвета	Эмпирические частоты	Эмпирические частости	Накопленные эмпирические частости	Разность ∑f^₁-∑f^₂
f₁	f₂	f^*₁	f^*₂	∑f^*₁	∑f^*₃
			0,235	0,123	0,235	0,123	0,112
			0,147	0,141	0,382	0,264	0,118
			0,128	0,145	0,510	0,409	0,101
			0,078	0,109	0,588	0,518	0,070
			0,147	0,114	0,735	0,632	0.103
			0,098	0,140	0,833	0,772	0,061
			0,088	0,121	0,921	0,893	0,028
			0,079	0.107	1,000	1,000
Суммы			1,000	1,000

Максимальная разность между накопленными эмпирическими частостями составляет 0,118 и падает на второй разряд.

В соответствии с пунктом 8 алгоритма 15 подсчитаем значение λ:

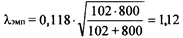По таблице 17-Б приложения 1 определяем уровень статистической значимости полученного значения: р = 0,16.

Построим для наглядности ось значимости.

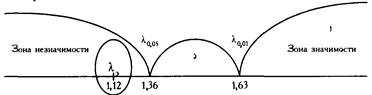
На оси указаны критические значения λ, соответствующие принятым уровням значимости: λ_0,05= 1,36, λ_0,01= 1,63.

Зона значимости простирается вправо, от 1,63 и далее, а зона незначимости – влево, от 1,36 к меньшим значениям.

λ_эмп< λ_кр^.

Ответ: H₀ принимается. Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара совпадают. Таким образом, распределения желтого цвета в двух выборках не различаются, но в то же время они по-разному соотносятся с равномерным распределением: у Клара отличий от равномерного распределения не обнаружено, а в отечественной выборке различия обнаружены (р < 0,05).

<49 50 515253 54 55 >

Дата добавления: 2021-11-16; просмотров: 277;