Показателей недостаточности
| Группы | «Есть эффект», показатель недостаточности равен 0 или > 30 | «Нет эффекта», показатель недостаточности от 5 до 25 | Суммы |
| 1 группа – с большей энергией вытеснения | 16 (88,9%) | 2 (11.1%) | |
| 2 группа – с меньшей энергией вытеснения | 8 (33,3%) | 16 (66,7%) | |
| Суммы | 423 |
В первоначальной выборке было 50 человек, но 8 из них были исключены из рассмотрения как имеющие средний балл по показателю энергии вытеснения (14-15). Показатели интенсивности чувства недостаточности у них тоже средние: 6 значении по 20 баллов и 2 значения по 25 баллов.
По таблице 18 приложения 1 определим величины φ, соответствующие сопоставляемым процентным долям:
φ1(88,9%) = 2,462
φ2(33,3%) = 1,230.
Подсчитаем эмпирическое значение φ*:
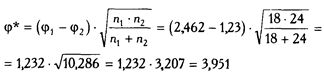
Критические значения φ* при любых n1, n2, как мы помним из предыдущего примера, составляют:
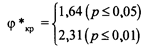
φ*эмп = 3,951
φ*эмп > φ*кр (р ≤ 0,01).
Таблица 19 приложения 1 позволяет нам и более точно определить уровень значимости полученного результата: р < 0,001.
Ответ: Н0 отвергается. Принимается Н1. Крайние значения показателя недостаточности (либо 0, либо 30 и более) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энергией вытеснения.
Итак, испытуемые с большей энергией вытеснения могут иметь как очень высокие (30 и более), так и очень низкие (нулевые) показатели ощущения собственной недостаточности. Можно предположить, что они вытесняют и свою неудовлетворенность, и потребность в жизненном успехе. Эти предположения нуждаются в дальнейшей проверке.
Полученный результат, независимо от его интерпретации, подтверждает возможности критерия φ* в оценке различий в форме распределения признака в двух выборках.
В мощных возможностях критерия φ* можно убедиться, подтвердив совершенно иную гипотезу при анализе материалов данного примера. Мы можем доказать, например, что в группе с большей энергией вытеснения показатель недостаточности все же выше, несмотря на парадоксальность его распределения в этой группе.
Сформулируем новые гипотезы
Н0: Наиболее высокие значения показателя недостаточности (30 и более) в группе с большей энергией вытеснения встречаются не чаще, чем в группе с меньшей энергией вытеснения.
Н1: Наиболее высокие значения показателя недостаточности (30 и более) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энергией вытеснения.
Построим четырехпольную таблицу, используя данные таблицы 14.4.
По таблице 18 приложения 1 определяем величины φ:
φ1(61,1%) = 1,795
φ2(25,0%) = 1,047.
Подсчитываем эмпирическое значение φ*:

По таблице 19 приложения 1 определяем, что этот результат соответствует уровню значимости р = 0,008.
Ответ: Н0 отвергается. Принимается Н1. Наиболее высокие показатели недостаточности (30 и более баллов) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энергией вытеснения (р = 0,008).
Таблица 14.6
Четырехклеточная таблица для расчета критерия φ* при сопоставлении групп с большей и меньшей энергией вытеснения по уровню показателя
Недостаточности
| Группы | «Есть эффект», показатель недостаточности больше или равен 30 | «Нет эффекта», показатель недостаточности меньше 30 | Суммы |
| 1 группа – с большей энергией вытеснения | 11 (61,1%) | 7 (38,9%) | |
| 2 группа – с меньшей энергией вытеснения | 6 (25,0%) | 18 (75,0%) | |
| Суммы |
Итак, нам удалось доказать и то, что в группе с более энергичным вытеснением преобладают крайние значения показателя недостаточности, и то, что больших своих значений этот показатель достигает именно в этой группе.
Теперь мы могли бы попробовать доказать, что в группе с большей энергией вытеснения чаще встречаются и более низкие значения показателя недостаточности, несмотря на то, что средняя величина в этой группе больше (26,11 против 15,42 в группе с меньшим вытеснением).
Сформулируем гипотезы
Н0: Самые низкие показатели недостаточности (нулевые) в группе с большей энергией вытеснения встречаются не чаще, чем в группе с меньшей энергией вытеснения.
H1: Самые низкие показатели недостаточности (нулевые) встречаются в группе с большей энергией вытеснения чаще, чем в группе с менее энергичным вытеснением. Сгруппируем данные в новую четырехклеточную таблицу.
Таблица 14.7
Четырехклеточная таблица для сопоставления групп с разной энергией вытеснения по частоте нулевых значений показателя недостаточности
| Группы | «Есть эффект», показатель недостаточности равен 0 | «Нет эффекта», показатель недостаточности не равен 0 | Суммы | ||
| 1 группа – с большей энергией вытеснения | 5 (27,8%) | 13 (72,2%) | |||
| 2 (8.3%) | 22 (91,7%) | |||
| Суммы |
Определяем величины φ и подсчитываем значение φ*:
φ1(27,8%) = 1,111
φ2(8,3%) = 0,584.
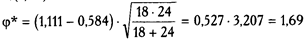
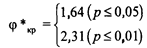
φ*эмп > φ*кр (р ≤ 0,05).
Ответ: Н0 отвергается. Самые низкие показатели недостаточности (нулевые) в группе с большей энергией вытеснения встречаются чаще, чем в группе с меньшей энергией вытеснения (р < 0,05).
В сумме полученные результаты могут рассматриваться как свидетельство частичного совпадения понятий комплекса у З. Фрейда и А. Адлера.
Существенно при этом, что между показателем энергии вытеснения и показателем интенсивности ощущения собственной недостаточности в целом по выборке получена положительная линейная корреляционная связь (r = +0,491, р < 0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.
Пример 4. Использование критерия φ* в сочетании с критерием λ Колмогорова-Смирнова в целях достижения максимально точного результата
Если выборки сопоставляются по каким-либо количественно измеренным показателям, встает проблема выявления той точки распределения, которая может использоваться как критическая при разделении всех испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта».
В принципе точку, по которой мы разделили бы группу на подгруппы, где есть эффект и нет эффекта, можно выбрать достаточно произвольно. Нас может интересовать любой эффект, и, следовательно, мы можем разделить обе выборки на две части в любой точке, лишь бы это имело какой-то смысл.
Для того чтобы максимально повысить мощность критерия φ*, нужно, однако, выбрать точку, в которой различия между двумя сопоставляемыми группами являются наибольшими. Точнее всего мы сможем сделать это с помощью алгоритма расчета критерия λ, позволяющего обнаружить точку максимального расхождения между двумя выборками.
Возможность сочетания критериев φ* и λ описана Е. В. Гублером [13]. Попробуем использовать этот способ в решении следующей задачи.
В совместном исследовании М. А. Курочкина, Е. В. Сидоренко и Ю. А. Чуракова (1992) в Великобритании проводился опрос английских общепрактикующих врачей двух категорий: а) врачи, поддержавшие медицинскую реформу и уже превратившие свои приемные в фондодержащие организации с собственным бюджетом; б) врачи, чьи приемные по-прежнему не имеют собственных фондов и целиком обеспечиваются государственным бюджетом. Опросники были разосланы выборке из 200 врачей, репрезентативной по отношению к генеральной совокупности английских врачей по представленности лиц разного пола, возраста, стажа и места работы – в крупных городах или в провинции.
Ответы на опросник прислали 78 врачей, из них 50 работающих в приемных с фондами и 28 – из приемных без фондов. Каждый из врачей должен был прогнозировать, какова будет доля приемных с фондами в следующем, 1993 году. На данный вопрос ответили только 70 врачей из 78, приславших ответы. Распределение их прогнозов представлено в таблице 14.8 отдельно для группы врачей с фондами и группы врачей без фондов.
Различаются ли каким-то образом прогнозы врачей с фондами и врачей без фондов?
Таблица 14.8
Дата добавления: 2021-11-16; просмотров: 447;











