Сопоставление эмпирического распределения

С теоретическим

Пример 13.12. В выборке здоровых лиц мужского пола, студентов технических и военно-технических вузов в возрасте от 19-ти до 22 лет, средний возраст 20 лет, проводился тест Люшера в восьмицветном варианте. Установлено, что желтый цвет предпочитается испытуемыми чаще, чем отвергается (табл. 13.15). Можно ли утверждать, что распределение желтого цвета по восьми позициям у здоровых испытуемых отличается от равномерного распределения?

Таблица 13.15

Эмпирические частоты попадания желтого цвета на каждую
из 8 позиций (n = 102)

Сформулируем гипотезы

H₀: Эмпирическое распределение желтого цвета по восьми позициям не отличается от равномерного распределения.

H₁: Эмпирическое распределение желтого цвета по восьми позициям отличается от равномерного распределения.

При решении будем опираться на следующий алгоритм.

АЛГОРИТМ

расчета абсолютной величины разности d между
эмпирическим и равномерным распределениями

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2. Подсчитать относительные эмпирические частоты (частости) для каждого разряда по формуле:

,

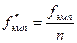где f_эмп – эмпирическая частота по данному разряду;

n – общее количество наблюдений.

Занести результаты во второй столбец.

3. Подсчитать накопленные эмпирические частости 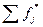по формуле:

,

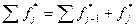где 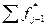– частость, накопленная на предыдущих разрядах;

j – порядковый номер разряда;

– эмпирическая частость данного j-го разряда.

Занести результаты в третий столбец таблицы.

4. Подсчитать накопленные теоретические частости для каждого разряда по формуле:

∑f*_{т j}=∑f*_{т j-1}+f*_{т j},

где ∑f*_тj-1 – теоретическая частость, накопленная на предыдущих разрядах;

j – порядковый номер разряда;

f*_тj – теоретическая частость данного разряда.

Занести результаты в третий столбец таблицы.

5. Вычислить разности между эмпирическими и теоретическими накопленными частостями по каждому разряду (между значениями 3-го и 4-го столбцов).

6. Записать в пятый столбец абсолютные величины полученных разностей без их знака. Обозначить их как d.

7. Определить по пятому столбцу наибольшую абсолютную величину разности – d_max.

8. По таблице 17-А приложения 1 определить или рассчитать критические значения d_max для данного количества наблюдений n.

Если d_max равно критическому значению d или превышает его, различия между распределениями достоверны.

Теперь приступим к расчетам, постепенно заполняя результатами таблицу расчета критерия λ. Все операции лучше прослеживать по таблице 13.16, тогда они будут более понятными.

Занесем в таблицу наименования (номера) разрядов и соответствующие им эмпирические частоты (первый столбец таблицы 13.16).

Затем рассчитаем эмпирические частости f* по формуле:

,

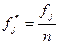где f_j – частота попадания желтого цвета на данную позицию;

n – общее количество наблюдении;

j – номер позиции по порядку.

Запишем результаты во второй столбец (табл. 13.16).

Теперь нам нужно подсчитать накопленные эмпирические частости ∑f*. Для этого будем суммировать эмпирические частости f*. Например, для 1-го разряда накопленная эмпирическая частость будет равняться эмпирической частости 1-го разряда, ∑f*_j = 0,235 . (Все формулы приведены для дискретных признаков, которые могут быть выражены целыми числами, например: порядковый номер, количество испытуемых, количественный состав группы и т.п.)

Для 2-го разряда накопленная эмпирическая частость будет представлять собой сумму эмпирических частостей 1-го и 2-го разрядов:

∑f^*₁₊₂ = 0,235 + 0,147 = 0,382.

Для 3-го разряда накопленная эмпирическая частость будет представлять собой сумму эмпирических частостей 1-го, 2-го и 3-го разрядов:

∑f^*₁₊₂₊₃ = 0,235 + 0,147 + 0,128 = 0,510.

Мы видим, что можно упростить задачу, суммируя накопленную эмпирическую частость предыдущего разряда с эмпирической частостью данного разряда, например, для 4-го разряда:

∑f^*_1+2+3+4 = 0,510 + 0,078 = 0,588.

Запишем результаты этой работы в третий столбец.

Теперь нам необходимо сопоставить накопленные эмпирические частости с накопленными теоретическими частостями. Для 1-го разряда теоретическая частость определяется по формуле:

f^*_теор = 1/k,

где k – количество разрядов (в данном случае – позиций цвета).

Для рассматриваемого примера:

f^*_теор = 1/8 = 0,125.

Эта теоретическая частость относится ко всем восьми разрядам. Действительно, вероятность попадания желтого (или любого другого) цвета на каждую из восьми позиций при случайном выборе составляет 1/8, т. е. 0,125.

Накопленные теоретические частости для каждого разряда определяем суммированием. Для 1-го разряда накопленная теоретическая частость равна теоретической частости попадания в разряд:

f^*_{т 1} = 0,125.

Для 2-го разряда накопленная теоретическая частость представляет собой сумму теоретических частостей 1-го и 2-го разрядов:

f^*_{т 1+2} = 0,125 + 0,125 = 0,250.

Для 3-го разряда накопленная теоретическая частость представляет собой сумму накопленной к предыдущему разряду теоретической частости с теоретической частостью данного разряда:

f^*_{т 1+2+3} = 0,250 + 0,125 = 0,375.

Можно определить теоретические накопленные частости и путем умножения:

Sf^*_тj= f^*_теор∙j,

где f*_теор – теоретическая частость;

j – порядковый номер разряда.

Занесем рассчитанные накопленные теоретические частости в четвертый столбец таблицы (табл. 13.16).

Теперь нам осталось вычислить разности между эмпирическими и теоретическими накопленными частостями (столбцы 3-й и 4-й). В пятый столбец записываются абсолютные величины этих разностей, обозначаемые как d.

Определим по столбцу 5, какая из абсолютных величин разности является наибольшей. Она будет называться d_max. В данном случае d_max =0,135.

Теперь нам нужно обратиться к таблице 17-А приложения 1 для определения критических значений d_max при n = 102.

Таблица 13.16