Подходы по формированию уравнений множественной регрессии
Множественная регрессия – это уравнение связи с несколькими независимыми переменными, т.е.
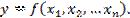 (4.1)
(4.1)
где y – зависимая переменная (результативный признак);
x1, x2, …, xn - независимые переменные (факторы).
Для построения уравнения множественной регрессии чаще всего используются следующие функции:
линейная – 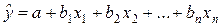
степенная – 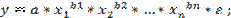 (4.2)
(4.2)
экспонента – 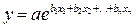
гипербола – 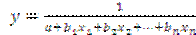 .
.
Для оценки параметров уравнения множественной регрессии также используется МНК, сущность которого заключается в составлении системы нормальных уравнений, их преобразований и последующего нахождения параметров регрессии.
На практике часто используют другой подход по определению параметров множественной регрессии, сущность которого заключается в построении на начальном этапе исследования уравнения регрессии в стандартизированной форме и дальнейших его преобразований в ходе последующих этапов.
Уравнение множественной регрессии в стандартизованной форме имеет вид:
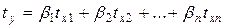 , (4.3)
, (4.3)
где 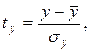
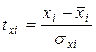 - стандартизованные переменные;
- стандартизованные переменные;
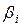 - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии.
Особенностью уравнения вида (4.3) является то, что к нему применимы положения метода наименьших квадратов.
Стандартизованные коэффициенты регрессии определяются из следующей системы уравнений:
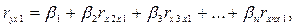
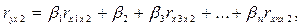 (4.4)
(4.4)
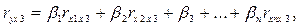
………………………………………………………….
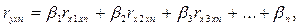
где ryx1, ryx2,… ryxn, rx1x2, rx3x2,… rxnx1 – частные коэффициенты линейной корреляции;
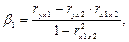
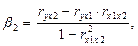
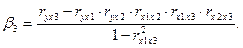 (4.5)
(4.5)
Связь коэффициентов множественной регрессии bi со стандартизованными коэффициентами βi описывается соотношением:
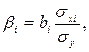 (4.6)
(4.6)
где σxi, σy – средние квадратические отклонения соответственно факторов xi и результативного фактора y.
Из выражения (4.6) получаем формулу перехода от коэффициентов βi к коэффициентам bi, необходимую для построения уравнений регрессии в естественной форме
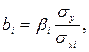 (4.7)
(4.7)
Параметр a применительно к уравнению множественной линейной регрессии (4.2) определяется по формуле (4.8):
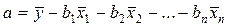 . (4.8)
. (4.8)
Таким образом, на основе проведенных вычислений определяются все составляющие уравнения множественной регрессии в естественной форме (4.2)
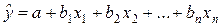 .
.
Дата добавления: 2018-05-10; просмотров: 877;











