Особенности применения нелинейных регрессионных моделей
Разнообразие нелинейных моделей, описывающих динамику социально-экономических явлений велико:
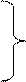
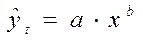 - степенная и показательная модели;
- степенная и показательная модели;
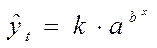
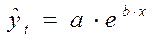 - экспоненциальная модель;
- экспоненциальная модель;
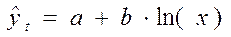 - логарифмическая модель;
- логарифмическая модель;
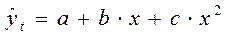 - модель на основе параболы второй степени;
- модель на основе параболы второй степени;
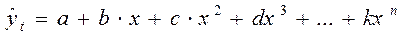 - полиномиальная модель.
- полиномиальная модель.
Среди множества нелинейных регрессионных моделей наиболее широкое распространение в эконометрических исследованиях получили полиномиальные модели.
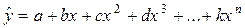 , (3.1)
, (3.1)
где y – результативная (зависимая) переменная (фактор-результат);
x – независимая переменная (фактор-признак);
a, b, c, d,…,k – параметры модели.
Основными этапами эконометрического исследования применительно к нелинейному регрессионному анализу являются следующие:
выбор формы уравнения взаимосвязи исследуемых факторов;
определение параметров уравнения регрессии;
оценка тесноты взаимосвязи (корреляции) исследуемых факторов;
оценка адекватности (статистической значимости) уравнения регрессии.
Кроме указанного, прикладные исследования могут включать этапы, связанные с проведением аналитического прогноза единичных значений результативной переменной, а также оценкой точности и достоверности прогноза.
Процедуру определения параметров нелинейной регрессии рассмотрим на примере параболы второй степени
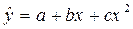 . (3.2)
. (3.2)
Учитывая линейность формы уравнения параболы, ее параметры также могут быть оценены методом наименьших квадратов (МНК):
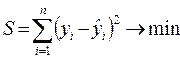 .
.
В данном случае на основе МНК образуется система нормальных уравнений, имеющая следующий вид (3.3):
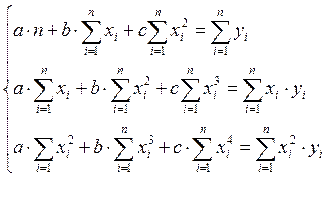 (3.3)
(3.3)
Метод подстановок в данном случае будет значительно громоздким и трудоемким с точки зрения вычислений, поэтому решим систему (3.3) методом Крамера. Для этого представим систему (3.3) в матричном виде:
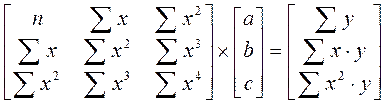 (3.4)
(3.4)
Неизвестные параметры a, bи cопределяются в результате решения системы (3.4)
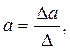
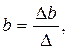
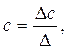 (3.5)
(3.5)
где Δ – главный определитель системы линейных уравнений (3.3) и (3.4);
Δa, Δb, Δc–частные определители системы линейных уравнений (3.3) и (3.4).
По найденным значениям параметров a, bи cзаписывается искомое уравнение параболы.
Процедура оценки тесноты взаимосвязи исследуемых факторов применительно к нелинейным регрессиям имеет некоторое отличие от исследований на основе линейных моделей. Вместо линейного коэффициента корреляции степень тесноты взаимосвязи факторов нелинейной регрессии оценивается на основе корреляционного отношения (η):
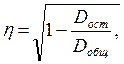 (3.6)
(3.6)
где Dост - остаточная дисперсия, определяемая из уравнения регрессии 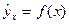 ;
;
Dобщ - общая дисперсия результативного признака (y);
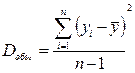 . (3.7)
. (3.7)
Величина показателя η находится в пределах: 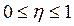 .
.
Оценка адекватности нелинейной регрессионной модели проводится на основе критерия Фишера по зависимостям (2.11) – (2.14), приведенным во втором разделе пособия.
В ходе процедуры дисперсионного анализа также целесообразно использовать таблицу вида 2.1.
В дополнение к процедурам оценки адекватности регрессионных моделей и дисперсионного анализа хотелось бы заметить, что, великому к сожалению, обозначения сумм квадратов в выражениях дисперсий в разных учебниках трактуются весьма своевольно. Так, по учебнику [Крыштановский А.О. "Анализ социологических данных с помощью пакета SPSS". - М., 2000. - 225 с.], сущность значений ESS и RSS определены с точностью наоборот:
ESS - Explained Sum of Squares;
RSS - Residuals Sum of Squares.
Такая путаница приводит к ошибочным формулам расчёта ESS и RSS, а также расчетам коэффициента детерминации (R-квадрата) и теоретических значений критерия Фишера. В качестве рекомендаций можно посоветовать использование русских обозначений дисперсий: факторная (Dфакт) и остаточная (Dост); рассчитывая их значения, исследователь точно будет знать используемые составляющие и их внутренне содержание.
Процедура эконометрического исследования на основе парной нелинейной регрессии детально рассмотрена на примере 3.1.
Пример 3.1.Имеются данные экспериментов по оценке прочностных свойств стеклопластика (фактор Y) в зависимости от температуры отверждения (фактор X) [11].
| № эксперимента | х | у |
| -3 | 5,3 | |
| -2 | 5,7 | |
| -1 | 6,1 | |
| 6,8 | ||
| 7,2 | ||
| 8,1 | ||
| 9,3 | ||
| 10,5 | ||
| 11,5 | ||
Требуется:1. Построить уравнение нелинейной регрессии, описывающей зависимость коэффициента прочности (Y) от температуры (X);
2. Оценить адекватность модели (с помощью коэффициента аппроксимации и по критерию Фишера);
3. Произвести прогноз значения коэффициента прочности при температуре отверждения 8 ºС.
С целью определения формы взаимосвязи исследуемых факторов построим поле корреляции, представленное на рисунке 3.1.
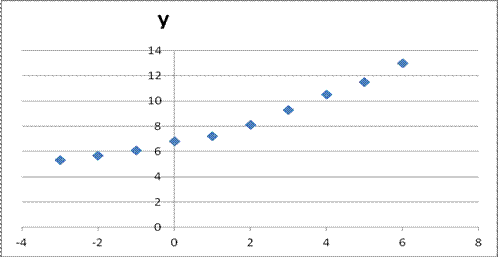
Рисунок 3.1 – Изображение поля корреляции значений прочностных свойств
стеклопластика (Y) от температуры отверждения (X).
По виду корреляционного облака сделаем предположение о полиномиальной форме взаимосвязи исследуемых факторов на основе параболы второй степени.
Для определения параметров нелинейного уравнения и решения задачи в целом воспользуемся методом Крамера; данные расчета коэффициентов системы нормальных уравнений (3.3) представим в виде таблицы 3.2
Таблица 3.2 – Данные расчета составляющих системы нормальных уравнений
| № эксп. | х | у | х2 | х3 | х4 | y∙х | y∙х2 | Yxi | (Yi-Yxi)2 | (Yxi-Yср)2 |
| -3 | 5,3 | -27 | -15,9 | 47,7 | 5,35 | 0,00215 | 9,02 | |||
| -2 | 5,7 | -8 | -11,4 | 22,8 | 5,65 | 0,002685 | 7,30 | |||
| -1 | 6,1 | -1 | -6,1 | 6,1 | 6,09 | 0,000166 | 5,12 | |||
| 6,8 | 6,66 | 0,018719 | 2,85 | |||||||
| 7,2 | 7,2 | 7,2 | 7,38 | 0,031104 | 0,95 | |||||
| 8,1 | 16,2 | 32,4 | 8,23 | 0,016044 | 0,02 | |||||
| 9,3 | 27,9 | 83,7 | 9,21 | 0,00738 | 0,75 | |||||
| 10,5 | 10,34 | 0,026038 | 3,95 | |||||||
| 11,5 | 57,5 | 287,5 | 11,60 | 0,010061 | 10,56 | |||||
| 13,00 | 8,26E-07 | 21,61 | ||||||||
| Сумма | 83,5 | 195,4 | 1123,4 | 0,114348 | 62,13 | |||||
| Среднее значение | 1,5 | 8,35 |
По результатам таблицы 3.2 запишем систему (3.4) в следующем виде:
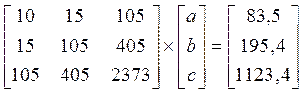 ,
,
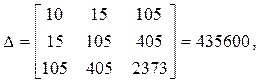
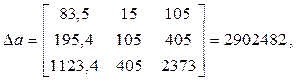
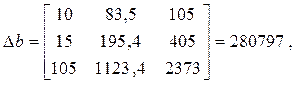
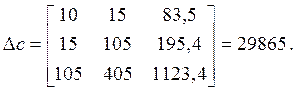 .
.
Параметры a, bи cполучаются в результате решения системы (3.4), а также выражений (3.5)
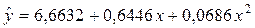 .
.
Расчетное значение критерия Фишера (Fрасч.) определяется по формуле (2.11) на основе данных расчета факторной и остаточной сумм квадратов (таблица (3.2))
Fрасч.= 1901,707.
Табличное (критическое) значение критерия (Fкр.) определяется на основе выражения (2.14) по данным приложения А, справочников [11,32] или таблицам Excel (раздел мастера функций «Статистические»): Fкр = (α=1-0,95; ν1= 2-1 ν2 = 10-3) = 4,737.
Так как расчетное значение критерия намного превосходит критическое, делаем вывод о правильности сделанного вначале исследований предположения о форме взаимосвязи прочностных свойств стеклопластика от температуры отверждения, а также о статистической значимости уравнения регрессии на основе параболы второй степени.
Прогноз значения коэффициента прочности стеклопластика при температуре отверждения 8 ºС произведем на основе полученного уравнения нелинейной регрессии путем подстановки значения x = 8: 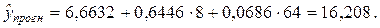
Для определения параметров других нелинейных регрессионных моделей используются подходы на основе линеаризации или замены переменных.
Дата добавления: 2018-05-10; просмотров: 1223;











