Законы постоянного тока
I. Электрический ток - направленное движение электрических зарядов. Если перемещаются элементарные заряды, например, электроны в металлах, ионы в газах и жидкостях, ток называется током проводимости. Если заряды много больше элементарных и связаны с макротелами, ток называется конвективным. Например, конвективный перенос объемного заряда в воздухе. Третьим случаем является электрический ток в вакууме. В настоящем параграфе речь пойдет только о токе проводимости.
Основной характеристикой тока является его величина i, определяющаяся отношением заряда, проходящего через поперечное сечение проводника, к времени:  . (8.1)
. (8.1)
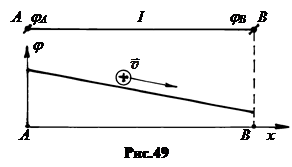 Если i = const, ток называют постоянным и обозначают I. Чтобы на отрезке проводника АВ существовал постоянный электрический ток, на концах проводника должна поддерживаться постоянная разность потенциалов
Если i = const, ток называют постоянным и обозначают I. Чтобы на отрезке проводника АВ существовал постоянный электрический ток, на концах проводника должна поддерживаться постоянная разность потенциалов  . (8.2)
. (8.2)
Направление тока соответствует направлению понижения потенциала, то есть направлению движения положительных зарядов (рис.49).
2. Закон Ома для участка цепи. В 1826 г. немец Георг Ом установил, что ток в проводнике прямо пропорционален напряжению U на его концах: 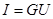 . (8.3)
. (8.3)
Здесь G - коэффициент пропорциональности, различный для разных проводников и называемый проводимостью.
Обратная проводимости величина R называется электрическим сопротивлением проводника постоянному току, R = 1çG. Формула закона Ома принимает вид:  (8.4)
(8.4)
Электрический ток, идущий в проводнике, пропорционален приложенному к концам проводника напряжению и обратно пропорционален сопротивлению проводника.
Единица тока в - ампер (А) - одна из 7 основных единиц в СИ. Единицу сопротивления ом (Ом) можно определить из закона Ома. Очевидно, [R] = [U]ç[I] то есть Ом = ВçА. Ом - это сопротивление такого проводника, в котором при напряжении на его концах 1 В идет ток 1 А.
Единица проводимости в СИ - сименс (Сим), Сим = Ом-1.
3. Электрическое сопротивление проводников имеющих длину l и постоянное сечение S, определяется формулой, найденной Гэмфри Дэви в 1821 г 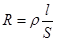 , (8.5)
, (8.5)
где ρ - коэффициент пропорциональности, называемый удельным сопротивлением проводника. Численно величина ρ равна сопротивлению R проводника единичной длины и единичного сечения. Единица ρ в СИ – Ом×м.
Опыт показывает, что удельное сопротивление металлов растет с температурой по закону, приближающемуся на отдельных участках к линейному  (8.6)
(8.6)
Здесь температурный коэффициент сопротивления, у чистых металлов приблизительно равен 1ç273 К-1, у сплавов может изменяться в широких пределах, вплоть до отрицательных значений. В таблице (8.1) приведены значения a некоторых металлов и сплавов при t = 20°С.
Если механически деформировать проводник, то изменение его геометрических размеров также влияет на величину его сопротивления. По этому принципу устроены электрические тензометры, позволяющие измерять быстропеременные механические напряжения.
4. Закон Ома в дифференциальной форме. Пусть к концам проводника длиной l и сечением S приложено напряжение U. Преобразуем формулу закона Ома.
| Таблица 8.1 | ||
| Вещество | r, мкОм×м | a, град-1 |
| Чистые металлы | ||
| Алюминий Al Вольфрам W Железо Fe Медь Cu Никель Олово Sn Платина Pt Ртуть Hg Серебро Au Цинк Zn | 0,028 0,055 0,098 0,017 0,973 0,120 0,105 0,958 0,016 0,059 | 0,0042 0,0048 0,0060 0,0043 0,0065 0,0044 0,0039 0,0010 0,0040 0,0042 |
| Сплавы и др. | ||
| Графит C | 8-20 | -0,0005 |
| Константан (Cu+ +Ni40%+Mn2%) | 0,50 | -0,00005 |
| Манганин (Cu+ +Ni3%+Mn2%) | 0,46 | 0,00001 |
| Нихром (Ni60%+ Cr20%+Mn1,5%+Fe) | 1,0 | 0,0001 |
 . (8.7)
. (8.7)
Отношение IçS = j - ток через единичное сечение проводника и называется плотностью тока. Отношение 1çr = g называется удельной электропроводностью. Единица g - Сим/м. Поскольку направление движения положительных зарядов совпадает с вектором напряженности Е, то выражение для плотности тока можно записать в векторной форме:  (8.8)
(8.8)
Это закон Ома в дифференциальной форме. Величины, входящие в него, определены в любой точке проводника.
5. Замкнутая электрическая цепь. Это система из источника тока, и электрически соединенных проводников различного сопротивления.
Источником тока называют элемент цепи, в котором происходит разделение электрических зарядов.
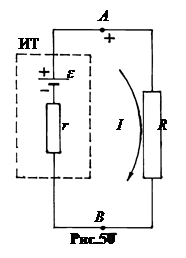 Разность потенциалов между точками А и В цепи создает электрическое поле в проводниках правой и левой частей цепи на рис.50. Если в цепи нет источника тока ИТ, то потенциалы точек А и В сравняются. Ток прекратится. Функция источника тока состоит в том, что он, перемещая заряды в левой части против поля АВ, поддерживает постоянной разность потенциалов между этими точками.
Разность потенциалов между точками А и В цепи создает электрическое поле в проводниках правой и левой частей цепи на рис.50. Если в цепи нет источника тока ИТ, то потенциалы точек А и В сравняются. Ток прекратится. Функция источника тока состоит в том, что он, перемещая заряды в левой части против поля АВ, поддерживает постоянной разность потенциалов между этими точками.
Силы, разделяющие заряды в ИТ, не являются кулоновскими, хотя, в конечном счете, имеют электромагнитную природу. В феноменологической теории эти силы принято называть сторонними. Процесс разделения зарядов сторонними силами совершается за счет какой-либо энергии. Например в генераторе электрической станции разделение происходит за счет механической энергии вращения ротора, а в гальваническом элементе разделение зарядов происходит за счет энергии химической реакции.
 6. Электродвижущая сила (ЭДС). Вычислим работу сторонних сил по перемещению заряда в цепи. Для этого введем в закон Ома в дифференциальной Форме вектор напряженности сторонних сил Eст :
6. Электродвижущая сила (ЭДС). Вычислим работу сторонних сил по перемещению заряда в цепи. Для этого введем в закон Ома в дифференциальной Форме вектор напряженности сторонних сил Eст :  или
или 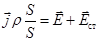 (8.9)
(8.9)
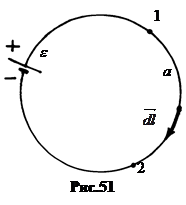
Здесь jS = I - ток в цепи, одинаковый во всех её участках. Умножим выражение (8.9) скалярно на элемент длины 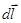 проводника вдоль по току и проинтегрируем от точки 2 до точки 2 по внешней части цепи, содержащий гальванический источник тока (рис.51).
проводника вдоль по току и проинтегрируем от точки 2 до точки 2 по внешней части цепи, содержащий гальванический источник тока (рис.51).
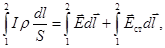 или
или  (8.10)
(8.10)
Полученная формула не несёт пока ничего нового. Она просто выражает закон Ома для участка цепи1-а-2, поскольку никаких сторонних сил на участке 1-а-2 в цепи с гальваническим источником тока нет и интеграл равен нулю. (Это не так в цепях, в которых действует ЭДС индукции). Но ситуация меняется, если точки 1 и 2 стянуть в одну так, чтобы одна из них пересекла источник тока. Тогда напряжение обратиться в нуль, U12 = 0 Сопротивление R12 перейдет в полное сопротивление цепи. Обычно его представляют как сумму сопротивлений источника тока r и внешней части цепи R. Выражение (8.10) принимает вид: 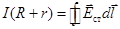 (8.11)
(8.11)
Интеграл по замкнутому контуру (его называют циркуляцией) вектора напряженности Eст здесь уже не равен нулю. Он определяет работу перемещения сторонними силами единичного положительного заряда по всей цепи. Эту работу называют электродвижущей силой источника тока и обозначают E. ЭДС - важнейшая характеристика ИТ. Как и напряжение она измеряется в вольтах.
7. Закон Ома для полной цепипредставлен формулой (8.11). Обозначив интеграл буквой E придадим ему привычный вид:  (8.12)
(8.12)
Ток в полной цепи пропорционален ЭДС источника тока E и обратно пропорционален полному сопротивлению цепи R + r.
Из формулы (8,12) следует, что ЭДС источника тока E равна сумме падений напряжений во внешней и во внутренней частях цепи  . (8.13)
. (8.13)
Напряжение во внешней части цепи IR = U легко измеряется вольтметром, присоединённым к зажимам источника тока, но измерить напрямую падение напряжения внутри источника тока Ir нельзя, его можно лишь уменьшить, уменьшая ток в цепи. В пределе при R®0 U®E Можно сказать, что ЭДС источника тока E равна напряжению на его зажимах, при разомкнутой цепи. Это условие реализуется при измерении ЭДС методом компенсации.
8 Тепловая мощность тока. Закон Джоуля-Ленца. При перемещении единичного заряда электрическими силами по цепи совершается работа, равная ЭДС источника. Если перемещаемый заряд равен q то работа его перемещения A = E q = E It = I2(R + r)t (8.14)
Эта работа состоит из двух частей: работы во внешней части цепи I2Rt и работы во внутренней части I2rt . Работа во внешней части называется полезной.
Полезная мощность Р, выделяющаяся во внешней части цепи, с учётом закона Ома для участка цепи может быть предусмотрена формулами: P = I2R = IU = U2çR (8.15)
Очевидно, формулы (8.15) позволяют вычислить электрическую мощность, выделяющуюся не только во всей внешней цепи, но и на любом элементе цепи, если из группы параметров I, R, U известны любые два.
Если бы заряды двигались в вакууме, то работа А пошла бы на увеличение скорости их движения, A→Eкин.При движении зарядов в проводнике скорость направленного движения зарядов практически не изменяется во времени, поскольку в противном случае происходило бы перераспределение концентрации зарядов по проводнику. Получается, что под действием постоянной электрической. силы заряды в проводниках дрейфуют с постоянной скоростью. Это напоминает движение частиц в вязкой среде. Следовательно, работа электрических сил идет на преодоления "вязкого сопротивления" проводника направленному движению зарядов и должна поэтому выделяться в виде тепла.
Количественную связь между выделяющимся в проводниках теплом Q на сопротивлении R и током I нашли опытным путем Джеймс .Джоуль (1841, индукционный метод) и Эмилий Ленц (1844, нагревание спирали) Q = I2Rt = IUt=  (8.16)
(8.16)
Связь между единицами тепловой мощности тока и напряжения очевидна: Вт = В×А, Дж = Вт×с = В×А×с .
9. Закон Джоуля-Ленца в дифференциальной форме определяет тепловую мощность, выделяющуюся в единице объема проводника.
Если по проводнику с удельной проводимостью g, длинной l и с постоянным сечением S проходит ток I, а на концах проводника напряжение U, то выделяющаяся в единице объёма проводника тепловая мощность равна 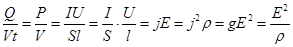 (8.17)
(8.17)
10. Разветвленные цепи. Вычисление взаимодействий. Разветвлёнными называются цепи, содержащие узлы - точки, в которых содержится более трёх проводников.
В простейшем случае разветвлённая цепь содержит один источник тока и группу сопротивлений. Поэтому задача сводится к вычислению сопротивлений отдельных участков цепи и всей цепи в целом. Исходными для вычисления являются правила:
а) Сопротивление участка цепи из последовательно соединенных проводников равно сумме сопротивлений этих проводников 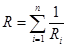 . (8.18)
. (8.18)
б) Проводимость участка цепи из параллельно соединённых проводников равна сумме проводимостей этих проводников  или
или 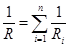 . (8.19)
. (8.19)
 Вся работа в дальнейшем сводится к разбиению цепи на такие однородные участки и подсчёту их сопротивлений. Схемы цепей полезно видоизменять, например, делая их более наглядными (рис.52-а), разделяя параллельные ветви в точках одинакового потенциала (рис.52-б), выбрасывая сопротивления, соединяющие эквипотенциальные точки и не вносящие вклада в проводимость цепи (риc.52-а и 52-в), рассекая цепь эквипотенциальными плоскостями на последовательные участки, состоящие из параллельно включенных сопротивлений (рис52-г).
Вся работа в дальнейшем сводится к разбиению цепи на такие однородные участки и подсчёту их сопротивлений. Схемы цепей полезно видоизменять, например, делая их более наглядными (рис.52-а), разделяя параллельные ветви в точках одинакового потенциала (рис.52-б), выбрасывая сопротивления, соединяющие эквипотенциальные точки и не вносящие вклада в проводимость цепи (риc.52-а и 52-в), рассекая цепь эквипотенциальными плоскостями на последовательные участки, состоящие из параллельно включенных сопротивлений (рис52-г).
Если все сопротивления на схеме (рис.52-а) одинаковы и равны R, то сопротивления цепи между точками A и B RАВ = R.
Если на остальных рисун-ках каждый прямой отрезок между узла-ми на схеме имеет сопротивление R, то на рис.52-б_ RАВ = 4Rç5. На рис.52-в RАВ = 6Rç7, на рисунке 52-г. RАВ = Rç2 + Rç4 + Rç6 + Rç6 + Rç4 + Rç2 = 11Rç6.
11. Разветвленные цепи. Правила Кирхгофа. В разветвленных электрических цепях, содержащих несколько источников тока, в разных участках, вычисление токов становится сложной задачей. Эти вычисления сильно упрощаются и формализуются, если пользоваться алгоритмом Кирхгофа, сформулированным им в идее двух правил:
 1-е. Сумма токов в узле равна нулю
1-е. Сумма токов в узле равна нулю 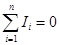 . (8.20)
. (8.20)
2-е. Сумма падений напряжений в контуре равна сумме действующих в контуре ЭДС.  (8.21)
(8.21)
Контуром называется кольцевой участок цепи. Первое правило выражает закон сохранения электрического заряда, второе закон Ома для замкнутой цепи.
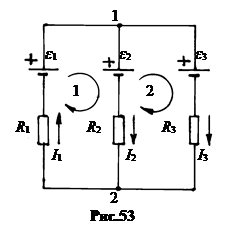
При решении задач произвольно задается направление токов и произвольно выбирается направление обхода в контурах. В качестве примера рассмотрим технологию вычисления токов в ветвях цепи, показанной на рисунке (рис.53). Полагаем значения всех сопротивлений и ЭДС всех источников тока известными.
Токи, идущие вдоль направления обхода, принимаются положительными, против - отрицательными. ЭДС, действующие в направлении обхода, также считаются положительными, а против - отрицательными.
Чтобы задача могла быть решена, общее число уравнений должно быть равным числу неизвестных токов. В начале составляются уравнения для узлов. Число независимых уравнений для токов в узлах на одно меньше количества узлов. Остальные недостающие уравнения составляются для контуров. Их число равно числу внутренних областей плоской схемы без взаимопересечений ветвей. Целесообразно в первую очередь составить уравнения для внутренних контуров, то есть минимальных. В схеме цепи на рис.53 уравнение для узлов должно быть одно. Полагаем токи, входящие в узел, положительными, выходящие - отрицательными. Тогда, например, для узла 1: I1 - I2 - I3 = 0 (8.22)
Всего неизвестных токов три, поэтому нужны ещё два уравнения. Составим их для внутренних контуров 1 и 2.
Контур 1: I1R1+ I2R 2 = E 1 - E 2 (8.23)
Контур 2: I2R2+ I3R3 = E 2 - E 3 (8.24)
Итак, имеем систему из трёх линейных уравнений с тремя неизвестными I1, I 2, I 3.
В принципе неизвестными могут быть и другие величины. Но для получения однозначного решения число неизвестных параметров должно быть равно числу независимых уравнений.
Напомним, что направление токов и обхода произвольны. Если какой-либо ток в решении окажется отрицательным, это значит, что его действительное направление противоположно в начале принятому.
Ток в металлах.
Природа носителей электрического тока в металлах была установлена в следующих экспериментах.
 а. Опыты Карла Рике, 1901г, состояли в том, что через 3 очень хорошо прошлифованных торцевыми поверхностями цилиндра медь - алюминий - медь в течении года пропускался электрический ток (рис.54). Суммарный прошедший заряд составлял 3,5×106 Кл. Взвешивание до и после опытов показала, что с точностью до 0,03мг масса цилиндров осталась неизменной. Это можно объяснить лишь тем, что электрический заряд в металлах переносится не ионами, а какими-то другими одинаковыми во всех металлах частицами.
а. Опыты Карла Рике, 1901г, состояли в том, что через 3 очень хорошо прошлифованных торцевыми поверхностями цилиндра медь - алюминий - медь в течении года пропускался электрический ток (рис.54). Суммарный прошедший заряд составлял 3,5×106 Кл. Взвешивание до и после опытов показала, что с точностью до 0,03мг масса цилиндров осталась неизменной. Это можно объяснить лишь тем, что электрический заряд в металлах переносится не ионами, а какими-то другими одинаковыми во всех металлах частицами.
б. Опыты Леонида Мендельштамма и Николая Папалекси, 1913г. Катушка с проводом, концы которого присоединены к телефону, приводилась в колебательное движение вокруг своей оси (рис.55). При этом телефон издавал звук с частотой, равной частоте колебаний катушки.
 Звучание телефона можно объяснить тем, что носители электрического заряда в металлах обладают инертной массой и сравнительно слабо связаны с кристаллической решеткой металла.
Звучание телефона можно объяснить тем, что носители электрического заряда в металлах обладают инертной массой и сравнительно слабо связаны с кристаллической решеткой металла.
в. Опыты Ричарда Толмена с сотрудниками (Т.Стюард). 1916-1926 г, развивали идеи Мендельштамма Папалекси и позволили получить первые количественные результаты.
Катушка с большим числом витков раскручивалась вокруг своей оси, а затем резко тормозилась. Концы провода катушки могли скручиваться и были присоединены к баллистическому гальванометру. Магнитное поле земли тщательно компенсировалось проводниками с током. При резком торможении катушки гальванометр давал отброс.
Если m - инертная масса носителей электрического заряда, а e -их заряд, то тормозное изменение импульса носителей зарядов равно (mN)dv = Fdt = (eN)Edt (9.1)
Здесь N число носителей зарядов в объеме провода катушки.
Разделив на N и приняв во внимание, что E = Uçl, где U - напряжение на концах провода, а l - его длина, и что U = Ri; где R - сопротивление цепи, а i - протекающий в цепи ток, получаем изменение импульса единичного носителя зарядов.
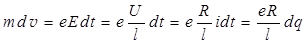 (9.2)
(9.2)
Проинтегрировав по времени торможения катушки, получаем:
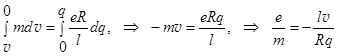 (9.3)
(9.3)
Линейная скорость вращения составляла v = 300 м/с, длинна провода катушки l = 500 м. Опыты с медной, алюминиевой, серебряной проволоками. При различных сопротивлениях цепи R и различных значениях измерявшегося гальванометром заряда q удельный заряд носителей оказался одинаковым и равным eçm = 1,6×1011 Кл/кг. Это было близко к результатам, полученным Дж. Томсоном двадцатью годами ранее в опытах с катодными лучами.
Обобщение результатов перечисленных ответов позволило сделать следующие выводы:
Носители электрических зарядов во всех металлах одинаковы;
Носители электрических зарядов в металлах вполне материальны, обладают инерцией и слабо связаны с кристаллической решеткой металла.:
Удельный заряд носителей составляет eçm = 1,6×1011 Кл/кг.
Поскольку к этому времени (конец 20-х годов XX века) Милликен определил элементарный заряд e = 1.6×10-19 Кл, то оказалось возможным оценить инертную массу носителей.  .
.
Носителями тока в металлах оказались электроны, обнаруженные ранее в катодных лучах (1897) и термоэлектронном облаке натриевых металлов. (1988, Т. Эдиссон).
В целом электропроводность следует рассматривать как явление переноса вещества и электрического заряда. Определяющим законом в последнем случае является закон Ома.
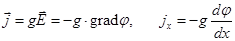 . (9.4)
. (9.4)
2.Электронная теория проводимости металлов. В первом десятилетии XX века Пауль Друде и Гендрик Лоренц построили классическую, т.е. основанную на уравнении Максвелла электронную теорию проводимости металлов.
Они исходили из того, что валентные электроны в металлах связаны со своими атомами настолько слабо, что могут легко перемещаться от одного атома к другому лишь за счет энергии теплового движения. Такая совокупность валентных электронов толковалась ими как электронный газ, подчиняющийся статике Максвелла Больцмана и являющийся по своим свойствам идеальным.
Идеальность электронного газа означает, что электроны проводимости не сталкиваются между собой, они соударяются лишь с узлами кристаллической решетки и находятся с ними в тепловом равновесии. Из этого условия можно оценить среднюю тепловую скорость электронов 
Рассмотрим, как объясняет теория проводимости Друде-Лоренца Законы Ома и Джоуля-Ленца. Для упрощения оценок полагаем, что все электроны проводимости имеют одинаковую скорость теплового движения - U.
а. Закон Ома. Если внутри металла создавать поле E, то на хаотическое движение электронов накладывается движение, направленное с некоторой средней скоростью дрейфа v. Ток, текущий в проводнике сечением S, равен I = enSv, где n концентрация электронов проводимости, e их заряд. Плотность тока 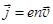 . (9.5)
. (9.5)
Найдем среднюю скорость дрейфа v. Будем полагать, что электрон под действием силы eE в промежуток времени t от одного соударения с узлом решетки до другого движется с ускорением a и увеличивает свою скорость от 0 до  . (9.6)
. (9.6)
Поскольку движение электрона в электрическом поле равноускоренное, то средняя скорость равна половине максимальной;  , (9.7)
, (9.7)
а плотность электрического тока равна  . (9.8)
. (9.8)
Формула (9.8) выражает закон Ома в дифференциальной форме в электронной теории. Коэффициент перед E расшифровывает макроскопическую характеристику проводника, удельную проводимость g через совокупность микрохарактеристик электронного газа.
Оценим среднее время t свободного пробега электронов проводимости на примере меди. Полагаем, что на каждый атом меди приходится один свободный электрон. Если M молярная масса меди, d ее плотность, то концентрация свободных электронов  . Подставив n в выражение удельной проводимости .
. Подставив n в выражение удельной проводимости .

В промежуток времени t между двумя соударениями электрон проходит среднее расстояние 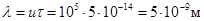 , что составляет несколько десятков поперечных атомов.
, что составляет несколько десятков поперечных атомов.
Оценим среднюю скорость дрейфа v электронов проводимости в меди при напряженности поля E = 0,1 Вçм. Из формулы (9.7) получаем:

Скорость дрейфа в миллиард раз меньше тепловой скорости u = 105 м/с.
Заметим, что напряженность E = 0.1 В/м не столь уж малая, как может показаться величина. Она соответствует напряжению 0,1 В на концах провода 1 м. При таком напряжении через медный провод сечением S = 1 мм2 проходит ток.
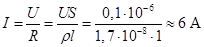
б. Закон Джоуля-Ленца. Масса электрона более чем в тысячу раз меньше массы атомов в узлах кристаллической решетки. Поэтому при неупругом соударении с узлом электрон останавливается, его скорость обращается в 0, а его кинетическая энергия дрейфа полностью отдается узлу. Так как в момент соударения 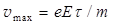 (формула 9.6), то энергия, отдаваемая электронами в единице объема в течении одной секунда, равна
(формула 9.6), то энергия, отдаваемая электронами в единице объема в течении одной секунда, равна
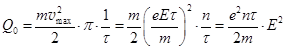 (9.9)
(9.9)
Эта энергия выделяется в виде тепла, поэтому формула (9.9) выражает закон Джоуля Ленца в дифференциальной форме. Выражение для удельной проводимости  (9.10)
(9.10)
получилось то же самое, что и в формуле закона Ома (9.8).
Строго говоря, предположение, что электрон отдает всю энергию при столкновении с атомом справедливо лишь тогда, когда атом покоится. Но атомы колеблются, а соударения не являются абсолютно неупругим. Поэтому электроны могут как отдавать энергию (соударение с убегающим атомом), так и получить ее (соударения с набегающим атомом). В статистике в условиях теплового равновесия средняя энергия движения электронов при постоянной температуре остается постоянной.
Но когда электронный газ приобретает направленную скорость дрейфа, он приобретает избыточную над тепловой энергию движения. Эта энергия электронов неравновесная с энергией узлов. Поэтому она непрерывно передается узлам кристаллической решетки, повышая температуру проводника.
в. Закон Видемана Франца. В 1853 году немцы Г.Ведеман и Р.Франц установили, что отношение теплопроводности c к электропроводности g при одной и той же температуре одинаково у всех металлов. В 1882году датский физик Людвик Лоренц показал, что это отно-шение пропорционально абсолютной температуре  Закон Видемана-Франца. (9.11)
Закон Видемана-Франца. (9.11)
Здесь L - коэффициент, одинаковый для всех металлов, его называют числом Лоренца.
Классическая электронная теория так объясняет этот закон.
Поскольку электроны очень подвижны, то можно полагать, что теплопроводность металлов обусловлено в основном теплопроводностью его электронного газа. Его коэффициент теплопроводности равен 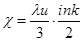 (9.12)
(9.12)
Здесь l- средняя длина свободного пробега электронов, u - их средняя скорость теплового движения, i = 3 - число степеней свободы электронов, k постоянная Больцмана.
Подставив в формулу (9.11) c из (9.12) и g из (9.10), где t =lçu, получаем: 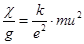 (9.13).
(9.13).
Из кинетической теории идеальных газов средняя скорость теплового движения электронов U2 = 8kTçpm. Отсюда  (9.14).
(9.14).
Классическая электронная теория в целом верно истолковывает закон Видемана Франца. Она расшифровывает число Лоренца L = 8k2çpm как комбинацию констант и прогнозирует линейную зависимость отношения cçg от температуры T.
4. Трудности классической электронной теории. Приведенные выше выводы принадлежат Друде и были сделаны им в предположении, что все электроны проводимости имеют одинаковую скорость u их теплового движения.
Генрик Лоренц уточнил выводы, приняв Максвеловское распределение электронов по скоростям. В результате в формуле закона Видемана Франца изменился коэффициент вместо 8çp = 2,55 стало ровно 2. Однако уточненная формула стала хуже соответствовать опыту.
а.Молярная теплоемкость металлов должна слагаться из теплоемкости узлов решетки 3R и теплоемкости идеального газа электронов 3Rzç2, где z число валентных электронов у атома. Полная теплоемкость получается равной 3R + 3Rzç2. Но опыт дает теплоемкость 3R (Закон Дюлонга и Пти). Классическая теория не объясняет этого.
В формуле удельной проводимости g = ne2l/2mu величина средней скорости u в соответствии со статистической теорией идеальных газов пропорциональна корню квадратному из температуры. Так как 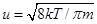 , то u ~
, то u ~  . Отсюда g = 1çr ~
. Отсюда g = 1çr ~ 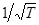 , или
, или  ~
~  . Но опыт дает линейную зависимость удельного сопротивления от температуры,
. Но опыт дает линейную зависимость удельного сопротивления от температуры, 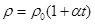 , или r ~ T. Расхождение необъяснимо.
, или r ~ T. Расхождение необъяснимо.
Совершенно не в состоянии классическая электронная теория объяснить явление сверхпроводимости. Суть его в том, что при определенной температуре, называемой критической Tк и близкой к абсолютному нулю у большинства химически чистых металлов, удельное сопротивление проводника падает скачком практически до нуля. Оценим, сделанные по времени затухания тока в сверхпроводящем кольце, показывает, что удельное сопротивление сверхпроводников не более 10-25 Ом×м. Для сравнения, удельное сопротивление меди в обычном состоянии равно 1,7×10-8 Ом×м.
В классической электронной теории r ~  , удельное сопротивление должно монотонно убывать с температурой, никакого скачка нет.
, удельное сопротивление должно монотонно убывать с температурой, никакого скачка нет.
5. Границы применимости электронной теории. Классическая теория электропроводности твердых тел тем сильнее расходится с экспериментом, чем ниже температура проводника и чем выше концентрация электронов проводимости. В тех случаях, когда температур достаточно высока, T > Tкомн, и концентрация носителей мала, использование электронной теории оправдано не только для качественных, но и для количественных оценок. Это очень ценная возможность, поскольку классическая электронная теория Друде-Лоренца много проще и нагляднее квантовой электронной теории.
Ток в электролитах
1. Электролиты - жидкие или твердые вещества, в которых присутствуют ионы, обуславливающие возможность прохождения электрического тока. Из жидких электролитов наиболее важны водные растворы кислот, солей и щелочей.
Молекулы растворяющихся веществ и молекулы растворителей, образующих электролиты, полярны. Их взаимодействие приводит к распаду молекул растворяющихся веществ на ионы. Этот процесс называется электролитической диссоциацией. Суть ее в том, что полярная молекула растворимого вещества, например, NaCl, разрывается полярными молекулами растворителя, например, воды H2O(рис.56).
 |
Вода имеет высокую диэлектрическую проницаемость,
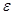 = 81. Поэтому электрическое взаимодействие между ионами молекул кислот, солей и щелочей ослабляется настолько сильно, что для распада молекул на отдельные ионы достаточно тепловой энергии движения молекул раствора.
= 81. Поэтому электрическое взаимодействие между ионами молекул кислот, солей и щелочей ослабляется настолько сильно, что для распада молекул на отдельные ионы достаточно тепловой энергии движения молекул раствора.
Молекулы воды являются жесткими диполями, они образуют вокруг свободных ионов устойчивую гидратную оболочку. Эта оболочка препятствует рекомбинации - обратному соединению ионов в нейтральные молекулы, и увеличивают сопротивление движению иона в растворе.
Доля распавшихся на ионы молекул растворенного вещества обозначается a и называется степенью электролитической диссоциации. Величина a может измеряться неэлектрическими методами, например, по величине осмотического давления. (Часть 2, §19).
2. Законы разбавления. С уменьшением концентрации раствора п коэффициент a растет. Зависимость a(п) установил Вильгельм Оствальд в 1888г., исходя из условия динамического равновесия процессов диссоциации и рекомбинации.
Для одноступенчатой диссоциации, когда молекула распадается на два иона, число распадов в единице объема раствора пропорционально числу нераспавшихся молекул и равно А(1 - a)п, где А коэффициент.
С другой стороны, число актов воссоединения пропорционально концентрации положительных ионов и концентрации отрицательных ионов и равно В(aп)2, где В коэффициент. В состоянии равновесия
А(1 - a)п = В(aп)2, 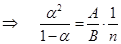 . Закон разбавления Оствальда, 1888. (10.1)
. Закон разбавления Оствальда, 1888. (10.1)
При п 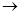 0 a
0 a 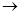 1.
1.
 1. Законы электролиза. Электролизом называют процесс прохождения через электролит электрического тока. В это явление входят также все процессы электрохимического окисления восстановления, происходящие на электродах в момент прохождения электрического тока. В результате на электродах выделяются продукты разложения раствора.
1. Законы электролиза. Электролизом называют процесс прохождения через электролит электрического тока. В это явление входят также все процессы электрохимического окисления восстановления, происходящие на электродах в момент прохождения электрического тока. В результате на электродах выделяются продукты разложения раствора.
Например, при электролизе воды на катоде выделяется газообразный водород, а на аноде газообразный кислород (рис.57).
На катоде: 4H+ + 4e → 2H2↑
На аноде: 4OH- - 4e → H2O + O2↑.
Положительные ионы, идущие на катод (отрицательный электрод), называются катионами. Отрицательные ионы, идущие на анод (положительный электрод), называются анионами.
а. Закон Ома для электролитов. Плотность электрического тока при направленном движении однозарядных частиц одного знака определяется формулой (9.5), 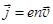 , где
, где  - скорость дрейфа частиц в электрическом поле. В электролитах есть заряды обоих знаков, поэтому плотность тока есть сумма:
- скорость дрейфа частиц в электрическом поле. В электролитах есть заряды обоих знаков, поэтому плотность тока есть сумма:  . (10.2)
. (10.2)
Если молекула распадается на два иона, то n+ = n- =an, где n концентрация молекул растворенного вещества, a - их степень диссоциации. Ионы двигаются в вязкой среде, их скорости пропорциональны напряженности поля 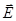 , так что
, так что 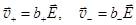 . Здесь b+ - подвижность положительных ионов, b- - подвижность отрицательных ионов. Так как скорость отрицательных ионов
. Здесь b+ - подвижность положительных ионов, b- - подвижность отрицательных ионов. Так как скорость отрицательных ионов  противоположна скорости положительных ионов
противоположна скорости положительных ионов  , то b- - отрицательное число. Полагая е- = - е+= - е, получаем:
, то b- - отрицательное число. Полагая е- = - е+= - е, получаем:
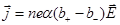 . Закон Ома для электролитов (10.3)
. Закон Ома для электролитов (10.3)
Оба слагаемые в скобках положительные числа. Коэффициент перед Е есть удельная электропроводность электролита.
Если в электролите не одно-, а многозарядные ионы с валентностью z, то коэффициент электропроводности увеличивается в z раз. g = znea(b+ - b-). (10.4)
Например, в растворе CuSO4 z =2, в растворе Al(NO3)3 z = 3.
С ростом температуры электропроводность электролитов увеличивается. В нешироком диапазоне температур эта зависимость приближается к линейной и может быть представлена эмпирической формулой: g = g25[1 + b(t - 25)]. (10.5)
Здесь g25 электропроводность при t = 25°С, b - температурный коэффициент. Для сильных кислот b = 0,0164, для сильных оснований b = 0,0190, для солей b = 0,0220.
Температурный рост электропроводности объясняется увеличением концентрации свободных ионов и увеличением их подвижности за счет падения вязкости раствора.
б. Законы Фарадея. Их два.
Первый закон: масса m выделившегося на электроде вещества пропорциональна заряду q, прошедшему через раствор, m = kq. (10.6)
Здесь k коэффициент пропорциональности, его наэывают электрохимическим эквивалентом вещества. Численно он равен массе вещества, выделившегося на электроде при прохождении через электролит 1 Кл электричества. Например, у серебра Ag k = 1,118 мгçКл, у меди Cu k = 0,329 мгçКл.
Второй закон: электрохимический эквивалент вещества k пропорционален его химическому эквиваленту Э, 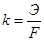 . (10.7)
. (10.7)
Здесь F коэффициент, его называют числом Фарадея.
Рассмотрим содержание второго закона. Если при осаждении на электроде массы m вещества прошел заряд q = Nez, где N число разрядившихся на электроде ионов, z их валентность, то k = mçq = mçNez. Но число молекул в массе m вещества равно N = NA(m/M), где M молярная масса вещества. Отсюда  . (10.8)
. (10.8)
Очевидно, химический эквивалент вещества Э есть отношение молярной массы вещества к валентности, Э = Mçz. Так, у водорода H Э = 1 гçмоль, у кислорода O Э = 16ç2 = 8 гçмоль, у кальция Са Э = 40ç2 = 20 гçмоль и т.д.
Число Фарадея F есть заряд, необходимый для осаждения на электроде 1 химического эквивалента любого вещества. F = 1,6×10-19×6× 1023 = 9,6 ×104 Кл.
4. Определение заряда ионов. Пользуясь законами Фарадея, можно определить заряд ионов разных веществ. Для этого нужно провести такой электролиз, в результате которого эти ионы, окисляясь или восстанавливаясь на электроде (отдают или принимают электроны), выделяются в виде нейтрального вещества выводятся из электролита.
Если масса выделившегося вещества m, то из законов Фарадея
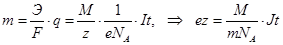 . (10.9)
. (10.9)
Таким путем можно определить кратность заряда иона по отношению к элементарному заряду. Например, ион водорода H+, его заряд
Дата добавления: 2018-05-10; просмотров: 1328;











