Пример 7.1 Электрическая ёмкость уединённого шара.

Выразив заряд q из формулы потенциала поверхности заряжённой сферы (4.10) и подставив его в формулу (7.6) получаем: 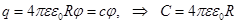(7.7)

Вычислим в качестве примера электрическую ёмкость земного шара в вакууме, где e = 1. Так как радиус земного шара R = 6,4·10⁶ м, то C=4pe₀R=4·3,14·8,85·10^-12·6,4·10⁶= =7,1·10^-4 Ф.

Как видно из этого примера единица ёмкости фарад очень большая величина. На практике чаще используются производные единицы микрофарад(10^-6 Ф), нанофарад(10^-9 Ф), и пикофарад(10^-12Ф).

3.Конденсаторы - технические устройства, позволяющие накапливать заряд и аккумулировать электрическое поле в сравнительно небольших замкнутых объемах. Первый конденсатор изобрёл Питер Мушенбрук в г. Лейдене в 1745 г. (лейденская банка).

Как следует из примера 7.1, электрическая ёмкость уединённых проводников очень мала. Даже у столь грандиозного тела как Земля она не превышает одного миллифарада. Поэтому электрические конденсаторы - устройства для накапливания электрического заряда - конструируются в виде системы из двух проводников, имеющих, как правило, одинаковую геометрическую конфигурацию и разделённых прослойкой диэлектрика.

В зависимости от формы этих двух проводников - их называют обкладками конденсатора, различают плоские, сферические и цилиндрические конденсаторы.

4.Плоский конденсатор. Представляет собой два плоских параллельных друг другу проводника, разделённых тонким слоем диэлектрика (рис.41). Расстояние между обкладками d обычно много меньше их площади S. В электрических устройствах обкладки конденсатора всегда заряжаются одинаковыми по величине, но противоположными по знаку зарядами.

Найдём поле в плоском конденсаторе и вычислим его электрическую ёмкость.

а. Поле в конденсатореПусть на обкладках конденсатора одинаковые по величине, но разные по знаку заряды с поверхностной плотностью σ, так что |σ₊| = |σ_-|. Левая обкладка на рис.41 заряжена положительно, правая - отрицательно.

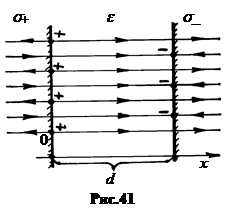При малом расстоянии d между обкладками их можно считать бесконечно протяжёнными заряженными плоскос-тями. Поля обкладок внутри конденсатора складываются, вне - взаимно уничтожаются. Из формулы поля бесконечной заряжённой плоскости (4.18), учитывая, что между обкладками находится диэлектрик с проницаемостью ε, получаем: 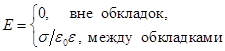(7.8)

Для вычисления потенциала точек поля внутри конденсатора полагаем потенциал отрицательной пластины равным 0. Ориентируем ось х по направлению силовых линий, начало совместим с положительной пластиной, тогда положение отрицательной пластины соответствует x = d.

Проинтегрируем выражение -dj =Edx от произвольной точки 0 < x < d до точки d.

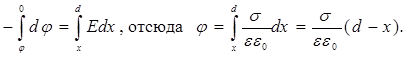(7.9)

Напряжение U между обкладками 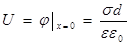(7.10)

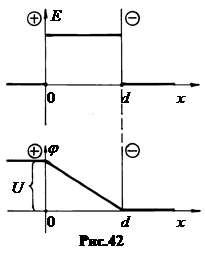
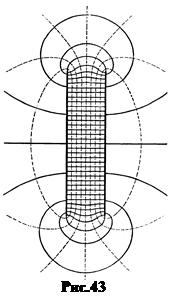На рисунке 42 показано поле Е внутри и вне плоского конденсатора (вверху) и потенциал поля j (внизу). На рис.43 показаны силовые линии и сечения плоскостью рисунка эквипотенциальных поверхностей (штриховые линии). Поле в плоском конденсаторе однородно. Лишь на краях обкладок наблюдается нарушение однородности из-за провисания поля наружу.

б. Электрическая ёмкость плоского конденсатора найдётся из формулы (7.6), где j = U напряжение между обкладками, определяемое формулой (7.10) 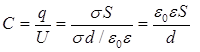. (7.11)

Для увеличения ёмкости конденсатора надо увеличивать площадь обкладок S, уменьшать расстояние d между ними и выбирать диэлектрик с максимально большой проницаемостью ε.

5.Сферический конденсаторобразуется двумя проводящими концентрическими сферами(рис.44-а). Поле в пространстве между сферами создаётся только внутренней сферой. Поэтому напряжённость и потенциал поля в интервале R₁< r < R₂ определяется формулами (4.9) и (4.10), записанными для случая ε ≠ 1(вместо e₀ входит произведение ee₀). Поле внутри малой сферы и вне большой равно 0 (рис.44-б).

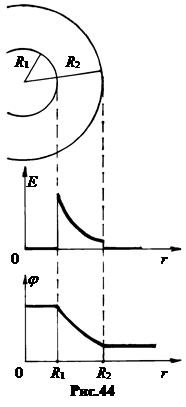Напряжение U между обкладками есть разность потенциалов поля точечного заряда между точками R₁ и R₂ (формула 4.10). 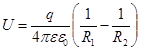(7.12)

Ёмкость сферического конденсатора 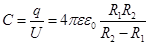. (7.13)

При R₂ ® ¥ получаем ёмкость уединённого шара (формула 7.7).

Сферические конденсаторы не имеют широкого технического применения. В основном они используются в научных исследованиях, например, при изучении внешнего фотоэффекта.

6.Цилиндрический конденсатор образуется двумя проводящими коаксиальными цилиндрами (рис.45-а). Как и в сферическом конденсаторе поле между цилиндрами создаётся только внутренним цилиндром. Напряжённость и потенциал в пространстве R₁> r >R₂ определяется формулами (4.23) и (4.25), записанными для случая диэлектрической сферы (вместо e₀ в формулы входит произведение ee₀)(рис.45-б).

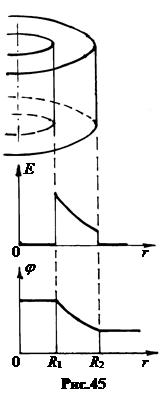Напряжение между обкладками найдётся из формулы (4.25), где r₀ = R₂, r = R₁. 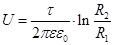(7.14)

Здесь t - заряд, приходящийся на единицу длины цилиндров. Ёмкость цилиндрического конденсатора на каждую единицу длины равна 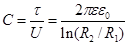(7.15)

Цилиндрические конденсаторы широко применяются в технических устройствах. Обычно они представляют собой керамическую трубку, на поверхности которой нанесены металлические слои, играющие роль обкладок. Формула (7.15) используется при вычислении волнового сопротивления коаксиальных кабелей.

Электрическая ёмкость элементов электрических устройств имеет часто большое значение для их нормального функционирования. Поэтому необходимо знание ёмкостей систем, не являющихся в обычном смысле конденсаторами. Примером такой системы является двухпроводная линия.

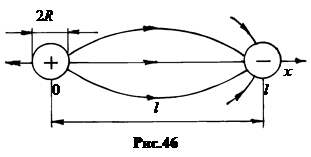Пример 7.2. Ёмкость двухпроводной линии. Пусть 2 параллельных провода имеют каждый диаметр 2R и расположены на расстоянии l друг от друга. Полагаем, что диаметр проводов много меньше расстояния между ними, 2R<< l. Это позволяет считать распределение заряда на каждом проводе равномерным, а поле невозмущённым и определяющимся формулами (4.23) и (4.25).

Пусть оба провода заряжены противоположными зарядами с одинаковой линейной плотностью t. Для вычисления напряжения между проводами направим ось х через центры проводов, начало оси выберем на левом положительном проводе (рис.46). Потенциал отрицательного провода примем за 0.

Напряжённость поля в любой его точке на оси х есть сумма

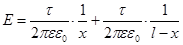, (7.16)

где e - диэлектрическая проницаемость сферы.

Проинтегрировав уравнение -dj = Edx от R до l - R, получаем напряжение между проводниками

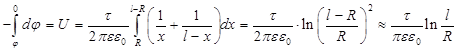(7.17)

Ёмкость двухпроводных линий увеличивает потери в энергосистемах и ограничивает максимальную частоту электрического поля в линиях связи.

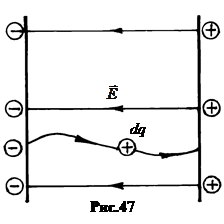7. Энергия заряженного конденсатора. Рассмотрим процесс зарядки конденсатора путём переноса одноимённых зарядов с одной обкладки на другую. Пусть с левой обкладки конденсатора на рис.47 переносятся положительные заряды. Перенос зарядов приводит к появлению поля в конденсаторе и должен совершаться за счёт работы внешних сил. Эта работа идёт на увеличение энергии электрического поля W.

dA = dW = Udq (7.19)

Но U = qçС, где q - заряд на правой по рис.47 обкладке, а С - ёмкость конденсатора. После интегрирования получаем :

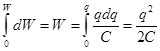(7.20)

Используя формулу q = СU, можно получить три выражения энергии

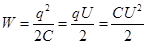(7.21)

8. Плотность энергии электрического поля. Если площадь пластин конденсатора велика, по сравнению с расстоянием между ними, то есть S >>d², то поле в плоском конденсаторе практически однородно и полностью заключено в объёме конденсатора V = Sd. Разделив энергию поля W на объем V, получаем плотность энергии электрического поля.

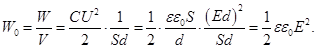(7.22)

Полученная формула определяет плотность энергии в зависимости от «точечной» характеристики поля напряжённости Е, поэтому применима не только к однородным, но и к неоднородным полям.

Пример 7.3. Размер электрона. Вычислим энергию электрического поля уединённой сферы, имеющей заряд q и радиус R, воспользовавшись формулой плотности энергии (7.22). Проинтегрируем энергию по всему объёму пространства вне шара.

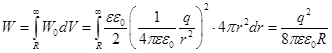(7.23)

С уменьшением радиуса сферы R энергия её поля стремится в бесконечность. Это обстоятельство ограничивает размер реальных зарядов снизу.

Например, если полагать, что вся масса покоя электрона m обусловлена его электрическим полем, то W = mc², где с скорость света в вакууме. Отсюда

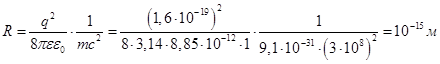
Это минимально возможный радиус электрона.

У частиц с большой массой, например, у протона, радиус может быть и меньше. Но предположение о том, что масса покоя частицы обусловлена исключительно её электрическим полем остаётся всего лишь гипотезой, которая не может объяснить массу нейтральных частиц, например, нейтронов.

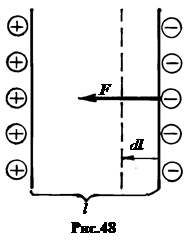9. Притяжение обкладок конденсатора. Поскольку обкладки имеют разный по знаку заряд, то они притягиваются друг к другу. Найдём силу притяжения обкладок плоского конденсатора, предположив, что одна из них смещается на расстояние dl за счёт энергии поля (рис.48).

Изменение энергии dW = dA = Fdl.

Отсюда 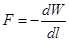. Но .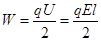

Тогда 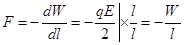. (7.24)

Знак «минус» означает, что пластины притягиваются.

10. Неустойчивость электростатических систем. В 1839 г. английский математик С. Ирншоу сформулировал и доказал теорему: совокупность неподвижных частиц, взаимодействующих между собой с силой, обратно пропорциональной квадрату расстояния (притягивающихся или отталкивающихся) не может образовывать устойчивой равновесной системы.

Доказательство теоремы Ирншоу основано на том, что потенциальная энергия системы электрически заряженных частиц не имеет минимума. Это значит, что совокупность неподвижных электрических зарядов, находящихся на конечном расстоянии друг от друга, не может находиться в устойчивом равновесии.

Теорема Ирншоу сыграла большую роль в развитии теории строения атома, поскольку из нее следует динамическая модель атома. Стационарный атом не может быть построен из неподвижных зарядов, связанных только электрическими силами.

Глава. 2. Законы постоянного тока и его природа в разных средах.