Магнитное взаимодействие электрических токов

1. Природный магнетизм(от греч. magnetis - магнит) известен людям с древности. Было давно замечено, что некоторые куски железных руд отталкиваются или притягиваются друг к другу в зависимости от взаимного положения. Подвешенные на нити или лежащие на поплавке на поверхности жидкости такие вытянутые куски самопроизвольно разворачивались в направлении север-юг. Это привело к изобретению компаса.

Научное изучение природного магнетизма началось в конце 16 века. Оказалось, что любой магнит имеет два разных полюса. Тот полюс, что указывал на север, назвали северным, а тот, что на юг – южным. Одноимённые полюса отталкиваются, а разноимённые притягиваются. Оказались безуспешными попытки разделением магнита получить одиночные магнитные полюса.

Стало ясно, что способность магнитных стрелок ориентироваться в направлении север-юг обусловлена тем, что Земля – большой магнит. В районе её северного географического полюса в точке с координатами 70°30¢ с.ш. и 97°41¢ в.д. находится южный магнитный и наоборот, в районе южного географического полюса в точке с координатами 73°39¢ ю.ш. и 146°15¢ з.д. находится северный магнитный полюс.

2.Закон Кулона для магнитных полюсов.В 1788 г. Шарль Кулон, экспериментируя с постоянными магнитами в виде длинных стержней, установил, что магнитные полюса взаимодействуют так же, как и электрические заряды.

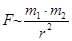. Закон Кулона для магнитных полюсов (12.1)

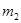Здесь и – количество магнетизма в полюсах (величины “магнитных зарядов”).

Однако вплоть до начала XIX в. не было опытных научных фактов, позволяющих говорить о существовании связи между электрическими и магнитными явлениями.

3.Открытие Эрстеда. В июле 1820 г. датский физик Ханс Эрстед открыл действие электрического тока на магнитную стрелку. “Гальваническое электричество, - писал он, - идущее с севера на юг над свободно подвешенной магнитной стрелкой, отклоняет её северный конец к востоку (рис.70-а), а проходя в том же направлении под стрелкой, отклоняет её к западу” (рис.70-б).

В опытах Эрстеда был открыт новый вид взаимодействия. До сих пор физика знала лишь центральные силы. Провод же с током не притягивал и не отталкивал магнитной стрелки. Он лишь поворачивал её вокруг оси.

Открытие Эрстеда побудило многих учёных к интенсивным исследованиям, в которых можно выделить два направления:

а. Изучение действия магнитного поля на проводник с током;

б. Изучение действия проводников с током на магнитную стрелку.

Опыты первой группы привели к открытию закона Ампера, опыты второй – к открытию закона Био-Савара-Лапласа.

4.Действие магнитного поля на ток. Поскольку проводник с током действует на магнитную стрелку, то это значит, что вокруг проводника с током возникает магнитное поле. Поэтому для изучения действия магнитного поля на ток можно использовать не только поля постоянных магнитов, но и создавать их с помощью электрических токов.

Ампер в своих опытах пошёл по второму пути. Он экспериментировал с прямоугольными рамками, по которым пропускались известной величины токи. Поскольку одна рамка (1 на рис.71) могла легко поворачиваться на оси, то можно было установить характер взаимодействия токов. Оказалось, что параллельные однонаправленные токи притягиваются, а противоположно направленные отталкиваются.

Для количественного описания взаимодействия тока с магнитным полем потребовалось ввести модель элемента тока (как материальная точка, точечный заряд и др.).

Элемент тока 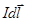есть произведение тока I на вектор 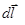, имеющий длину бесконечно малого отрезка проводника dl и направленный по току.

Результаты опытов Ампера и других исследователей позволили установить, что сила 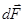действия магнитного поля на элемент тока 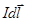определяется формулой.

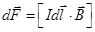. Формула Ампера, 1820 (12.2)

Вектор Bназывается магнитной индукцией и является основной характеристикой магнитного поля.

Если поле B однородно в пределах прямого провода длины l, то формула (12.2) легко интегрируется и принимает вид: 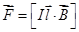или F = IlBsin( 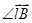). (12.3)

Определив величину и направление силы F, действующей на отрезок провода l c током I, можно найти величину и направление вектора индукции B.

Единица индукции в СИ – тесла (Тс). Если единице тесла приписать смысл в соответствии с формулой 12.3, то можно сказать, что 1 Тл – это индукция такого магнитного поля, в котором на проводник длиной 1 м с током 1 А, расположенный перпендикулярно вектору В, действует сила 1 Н.

5.Магнитное поле В, как и электрическое Е, можно графически изображать линиями. В каждой точке такой линии вектор В направлен по касательной. На практике направление линий В (силовых линий поля) определяются часто с помощью магнитной стрелки, которая располагается по касательной к линиям, или с помощью железных опилок. Оказалось, что система силовых линий поля постоянного магнита напоминает поле электрического диполя (рис.72), а магнитное поле прямого тока в любом нормальном к проводу сечении представляет собой систему концентрических окружностей (рис.73).

Магнитное поле, как и электрическое, подчиняется принципу суперпозиции. Если имеется несколько источников магнитного поля – электрических токов или постоянных магнитов, создающих по отдельности в некоторой точке индукции В₁, В₂, В₃ и т. д., то магнитная индукция суммарного поля в этой точке равна векторной сумме индукций отдельных полей.

. Закон сложения магнитных полей (12.4)

6.Магнитное поле элемента токаподробно изучали в 1920 г. французы Жан Био и Феликс Савар. Обработав их экспериментальный материал, Пьер Лаплас установил, что индукция dB магнитного поля элемента тока 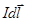в любой произвольной точке определяется формулой:

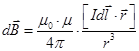. Закон Био-Савара-Лапласа, 1820г (12.5)

Здесь r- радиус-вектор, проведённый от элемента тока в ту точку поля А (рис.74), где определяется индукция; m ₀- размерный коэффициент пропорциональности, его называют магнитной постоянной. В системе единиц в СИ m ₀ = 4p×10⁻⁷ Гн/м точно. Величина m -магнитная проницаемость среды. Это безразмерное число, которое показывает, во сколько раз сила действия магнитного поля на проводник с током в данной среде больше силы действия в вакууме. В вакууме m =1, в ферромагнитных средах m >>1, в остальных m @1.

Силовые линии поля элемента тока представляют собой окружности, центры которых лежат на прямой MN, проходящей вдоль элемента тока. Направление силовых линий задаётся направлением вектора индукции dB. На практике его можно определить по правилу правого винта: если поступательное движение винта совпадает с направлением элемента тока Idl, то вращение винта происходит вдоль по силовой линии.

С увеличением расстояния r от элемента тока до точки поля А индукция убывает пропорционально 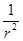. Поэтому густота линий поля с увеличением r быстро падает.

Вдоль прямой MN, на которой находится элемент тока Idl, поле равно нулю. Угол a между векторами Idl и r в этом случае равен нулю, и .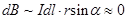

7. Проблема магнитных зарядов.В электрическом поле покоящихся зарядов силовые линии разомкнуты. Они начинаются на положительных и заканчиваются на отрицательных зарядах.

Замкнутость линий магнитного поля можно толковать как результат того, что в природе нет магнитных зарядов. Но возникает вопрос: что же является источником магнитного поля постоянных магнитов?

Андре Ампер высказал гипотезу, что источником магнитного поля во всех случаях являются электрические токи. Он предложил разделить учение об электричестве на два раздела: электростатику – учение о покоящихся зарядах и электродинамику – учение о движущихся зарядах. Магнетизм в системе Ампера – раздел электродинамики. Внутри постоянных магнитов, по мнению Ампера, циркулируют замкнутые микроскопические токи, которые и создают магнитное поле.

Эта глубокая догадка о замкнутых микротоках оставалась гипотезой почти в течение столетия, прежде чем в начале ХХ в. она получила опытное и теоретическое обоснование. Оказалось, что основным источником магнитного поля намагниченных тел является внутриатомное движение электронов.

Но поскольку магнитных зарядов в природе нет, то закон Кулона, описывающий взаимодействие магнитных полюсов (магнитных зарядов, как мыслилось в начале) теряет свою значимость и сохранят лишь историческое значение.

8.Взаимодействие элементарных токов. Закон Ампера. Если в формулу силы Ампера (12.2) вместо B подставить выражение индукции dB из закона Био-Савара-Лапласа (12.5), то получим формулу, определяющую силу dF взаимодействия двух элементарных токов. Присвоим элементу тока, создающему поле dB₁ (формула 12.5) индекс “1” , а элементу тока, испытывающему действие поля dB₂, индекс “2”. Тогда сила действия поля элемента тока I₁dl₁ на элемент тока I₂dl₂ определяется выражением.

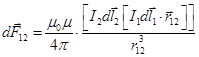. Закон Ампера для элементов тока (12.6)

Это основной закон электромагнетизма.

Если сравнить закон Ампера с законом Кулона для электрических зарядов, то можно увидеть как сходство, так и различие.

В законе Кулона характеристикой вещества является диэлектрическая проницаемость среды e, в законе Ампера – магнитная проницаемость среды m. Величина силы взаимодействия между электрическими зарядами убывает с квадратом расстояния между ними. Так же убывает величина силы взаимодействия между элементами тока. В законе Кулона 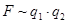, в законе Ампера .

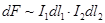Принципиальным отличием является то, что кулоновская сила – это центральная сила. Она всегда направлена вдоль прямой линии, проходящей через взаимодействующие заряды. Сила Ампера в данном случае не является центральной.

Рассмотрим несколько случаев.

а.Взаимодействие параллельных элементов тока. Чтобы вычислить силу dF₁₂ , действующую на элемент тока I₂dl₂, со стороны элемента I₁dl₁, надо найти вначале векторное произведение во внутренних скобках формулы 12.6 (рис.75). Вектор 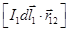направлен вниз. Переносим его к элементу I₂dl₂ и находим произведение .

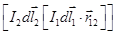Чтобы найти силу dF₂₁, действующую на элемент тока I₁dl₁ со стороны элемента I₂dl₂, надо от вектора r₁₂ перейти к вектору r₂₁, то есть направить его от элемента I₂dl₂ к элементу I₁dl₁. Вычислив 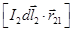и пристроив его к элементу I₁dl₁, находим произведение .

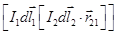Параллельные токи притягиваются с одинаковыми по величине силами, dF₁₂ = - dF₂₁.

б.Взаимодействие антипараллельных элементов тока (рис.76). Параллельные противоположно направленные токи отталкиваются с одинаковыми по величине силами, dF₁₂ = - dF₂₁.

в.Взаимодействие перпендикулярных токов. В случае скрещенных токов, показанном на рис.77, силы, действующие на оба элемента тока, равны нулю, dF₁₂ = - dF₂₁ = 0.

Однако могут быть случаи, когда при взаимодействии элементов тока 3-й закон Ньютона не выполняется (рис.78). Сила dF₂₁, действующая на элемент I₁dl₁, не равна нулю, dF₂₁ ¹ 0. Тогда как сила dF₁₂, действующая на элемент I₂dl₂, равна нулю, dF₁₂ = 0. Третий закон Ньютона нарушается.

Однако это нарушение относится к моделям – элементам тока. На опыте нельзя реализовать ограниченные по длине отрезки провода с током. Для замкнутых же проводников 3-й закон Ньютона выполняется совершенно точно.

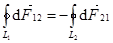. (12.7)

Здесь L₁ - контур первой замкнутой цепи с током I₁, L₂- контур второй замкнутой цепи с током I₂.

Пример 12.1 Магнитное поле конечного отрезка прямого тока.Вычислим индукцию поля B, создаваемого прямым отрезком провода с током I на некотором произвольном расстоянии R от провода в точке А (рис.79).

Поскольку магнитное поле подчиняется принципу суперпозиции, то индукцию поля в точке А можно найти как сумму индукций полей в точке А, создаваемых элементами токов Idl, уложенных вдоль всей длины провода.

По закону Био-Савара-Лапласа индукция поля элемента тока Idl в точке А, удалённой от элемента тока на расстояние r, есть 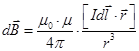. (12.8)

Пусть О – точка на проводе или на его продолжении, из которой построен перпендикуляр R в точку поля А. Положение точки О относительно элемента тока, определяется вектором 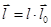, где - единичный вектор вдоль тока.

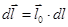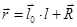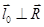Преобразуем выражение (12.8) к виду, удобному для интегрирования. Так как , , а , то 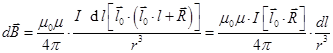. (12.9)

Коэффициент перед выражением 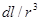не зависит от положения точки на проводе и выносится из-под знака интеграла. Для интегрирования выражения (12.9) надо от двух переменных l и r перейти к одной. В качестве переменной интегрирования выберем угол b между направлениями из точки А в точку О и в точку элемента тока. Тогда 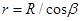, , 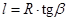. Подставляем: 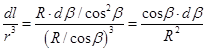. (12.10)

Проинтегрировав от угла b₁, под которым виден из точки А конец провода N, до угла b₂, под которым виден другой конец провода M, получаем: . (12.11)

Для модуля В формула упрощается: 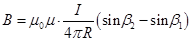. (12.12)

Для бесконечно длинного провода 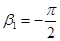, 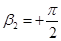и . (12.13)

9. Единица тока – ампер. Если поместить рядом два очень тонких параллельно расположенных провода бесконечной длины, расстояние между которыми R, токаждая точка одного провода будет находиться в постоянном магнитном поле другого. Силы, действующие на одинаковые отрезки l в любом месте любого провода одинаковы.

Допустим, для отрезка l₂ второго провода 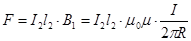. (12.14)

Данная ситуация используется для определения единицы тока в СИ – ампера. Если 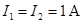, а , то в вакууме .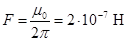

Ампер – сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает между ними силу, равную 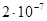ньютонов на каждый метр длины.