Вычисление магнитных полей

1.Поток вектора магнитной индукции (магнитный поток) Ф вводится так же, как поток вектора напряжённости электрического поля.

Магнитный поток dФ через элементарную площадку dS равен скалярному произведению векторов Bи dS×n: 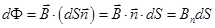, (13.1)

где n-единичный вектор нормали к площадке, - проекция вектора B на нормаль к площадке (нормальная к площадке составляющая вектора B) (рис.80).

Магнитный поток через конечную площадку находится интегрированием. . (13.2)

Если поле в пределах площадки однородно, а угол между векторами Bи n равен 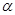, то поток через площадку

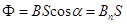. (13.3)

Единица магнитного потока в СИ – вебер (Вб), .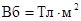

2.Теорема Гаусса для магнитных полей. Вычислим поток Ф вектора магнитной индукции B через замкнутую поверхность. Ограничимся простым случаем, когда поле создаётся бесконечным прямым током, а поверхностью является поверхность коаксиального с проводом цилиндра (рис.81).

Полный поток складывается из суммы потоков через боковую поверхность цилиндра и через его основания, Ф = Ф_бок + Ф_осн.

Магнитные силовые линии прямого тока есть окружности с центрами на проводе и лежащие в сечениях, нормальных проводу. Поэтому углы 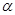между векторами B и нормалью к поверхности n во всех точках поверхности одинаковы и равны 90°.

Отсюда B_n = Bcosa = 0.

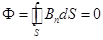. Теорема Гаусса для магнитного поля (13.4)

Поток вектора магнитной индукции через замкнутую поверхность равен нулю.

Результат не изменится, если поверхность имеет произвольную форму. Ведь её всегда можно охватить цилиндрической поверхностью. Поскольку линии не имеют разрывов, они не могут начинаться или кончаться между поверхностями. Но это значит, что магнитные потоки через обе замкнутые поверхности одинаковы и равны нулю.

Теорема Гаусса для магнитного поля (формула 13.4) выражает закон природы: магнитных зарядов в природе нет.

3.Циркуляция вектора B.Вычислим циркуляцию вектора индукции B магнитного поля по контуру, охватывающему прямолинейный ток. Для простоты интегрирования возьмём в качестве контура окружность радиуса R с центром на бесконечном проводе (рис.82).

Проекция вектора B на касательную к окружности равна модулю 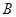, 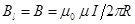. Отсюда

. (13.5)

Величина интеграла не изменяется, если контуром интегрирования будет любая замкнутая кривая какой угодно конфигурации.

Когда контур охватывает несколько потоков, то благодаря суперпозиции полей в правой части будет сумма токов. Причём, каждый ток считается столько раз, сколько раз он охватывается контуром (рис.83).

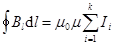. Теорема о циркуляции или закон полного тока (13.6)

Если направление тока совпадает с направлением обхода по правилу правого винта, ток берётся со знаком “плюс”, если не совпадает - со знаком “минус”. В примере рисунка 83 .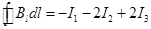

Теорема о циркуляции играет в электромагнетизме примерно такую же роль, как теорема Гаусса в электростатике. Она упрощает расчёт магнитных полей при наличии симметрии токов.

Исходным уравнением для вычисления магнитных полей постоянных токов является уравнение Био-Савара-Лапласа, имеющее элементарный характер. Задача в общем случае сводится к суммированию полей элементов тока, уложенных по всей длине данного проводника с током. Так вычислялось поле прямого тока в примере 12.1

В некоторых случаях симметричных токов можно воспользоваться результатами интегрирования, полученными в законе полного тока. В результате задача решается методами алгебры.

Пример 13.1.Магнитное поле внутри прямолинейного цилиндрического провода радиусом , Пусть по прямому цилиндрическому проводу радиусом течёт постоянный ток 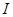. Плотность тока полагаем во всех точках одинаковой и равной j = IçS, где S = pR²- площадь сечения провода. Вычислим индукцию магнитного поля внутри провода на расстоянии от его оси (рис.84).

Воспользуемся законом полного тока. Вычислим циркуляцию вектора индукции B по окружности радиуса r. Из осевой симметрии тока следует, что индукция поля во всех точках окружности одинакова и равна B. Циркуляция вектора B по окружности радиуса r равна B×2pR.

По закону полного тока она пропорциональна току внутри этой окружности.

. (13.6)

Отсюда 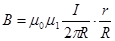. (13.7)

Здесь m₁- магнитная проницаемость вещества провода.

Индукция поля вне прямого бесконечного провода с током I определена в примере 12.1. Общее выражение для модуля индукции B поля прямого бесконечного тока запишется в виде:

(13.8)

Индукция магнитного поля максимальна на поверхности проводника. В центре проводника и на бесконечности от него индукция равна нулю (рис.85).

При использовании закона полного тока находится лишь модуль вектора B. Направление вектора B определяется из геометрии тока.

Пример 13.2. Магнитное поле внутри тороидальной катушки. Из соображений симметрии следует, что индукция B по величине одинакова во всех точках окружности радиуса R, центр которой лежит на оси AA тороида (рис.86). Поэтому циркуляция вектора индукции вдоль этой окружности равна B×2pR.. По закону полного тока она пропорциональна сумме токов, охватываемой этой окружностью. Очевидно 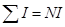, где N- полное число витков катушки. Отсюда 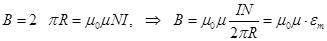(13.9)

Здесь 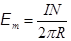- магнитодвижущая сила. Она равна произведению тока I на число витков катушки N, приходящееся на единицу длины тороида. Поле внутри тороида неоднородно. С увеличением радиуса окружности R оно убывает. Поле максимально вблизи внутренней поверхности тороида, радиус которой R₁, и минимально вблизи внешней поверхности тороида, радиус которой R₂.

Сравнив формулу (13.9) с формулой индукции поля прямого бесконечного тока (13.8), при r > R, можно сделать вывод, что поле внутри тороида такое же, как если бы оно создавалось прямым бесконечным током величиной NI, протекающим вдоль оси AA.

Пример 13.3. Поле внутри прямого бесконечного соленоида. Соленоидом называют катушку в виде намотанного на цилиндрическую поверхность изолированного провода, по которому течёт ток I (рис.87).

Найдём индукцию поля внутри бесконечного соленоида. Для этого воспользуемся законом полного тока.

В качестве замкнутого контура для вычисления циркуляции B возьмём прямоугольник ABCD, сторона АВ которого длиной l находится внутри соленоида и параллельна его оси ОО, а сторона CD бесконечно удалена.

Из соображений симметрии следует, что вектор B внутри соленоида параллелен его оси. Поэтому вклад в циркуляцию участка АВ равен B×l.

Участки ВС и DA перпендикулярны вектору B. Их вклад в циркуляцию равен нулю.

Сторона CD бесконечно удалена от соленоида. Поскольку поле каждого отдельного тока убывает с расстоянием, то на бесконечности оно равно нулю.

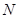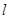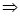
Если - число витков соленоида, приходящееся на отрезок его длины, то закон полного тока принимает вид: , 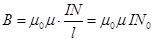. (13.10)

Здесь N₀- число витков, приходящееся на единицу длины соленоида.

Формула справедлива не только для соленоидов круглого, но и любого другого поперечного сечения. Внутри бесконечного соленоида поле однородно и параллельно оси соленоида. Силовые линии внутри соленоида идут в одну сторону, снаружи – в другую, внутри они пронизывают конечную площадь сечения соленоида, снаружи - бесконечное пространство. Поэтому плотность силовых линий вне бесконечного соленоида равна нулю. Поля вне соленоида нет, индукция равна нулю на любом от бесконечного соленоида расстоянии.

Пример 13.4. Поле кругового тока. Пусть проводник имеет форму окружности радиуса R. По проводнику течёт постоянный ток I. Вычислим магнитное поле на оси данного кругового тока в некоторой точке А, которая находится на расстоянии x от его центра (рис.88).

Вычисление циркуляции B по любому контуру здесь представляет собой сложную задачу. Применение закона полного тока малоэффективно. Поэтому будем решать задачу интегрированием закона Био-Савара-Лапласа.

Выберем два диаметрально противо-положных элемента тока Idl₁ и Idl₂ и определим суммарную индукцию их полей в точке А.

Нормальные к оси ОХ составляющие индукции dB_1n и dB_2n для каждой пары элементов токов взаимно уничтожаются, а составляющие вдоль оси ОХ суммируются. Так что . (13.11)

Здесь n- единичный правовращательный вектор площади контура, совпадающий здесь с положительным направлением оси ОХ.

Поскольку направление вектора dB определилось (вдоль оси ОХ), то в выражении закона Био-Савара-Лапласа для dB₁ (формула 12.5) оставляем только численную компоненту. Угол между любым элементом тока Idl и проведённым из него в точку А вектором r равен 90°. Поэтому 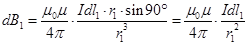. (13.12)

Индексы “1” и “2” у элементов тока и радиусов r были введены для упорядочения рисунка и рассуждений. Далее их опускаем. Приняв во внимание, что sinb = Rçr, интегрируем выражение (13.11) по половине длины окружности от 0 до pR (потому что два элемента тока). . (13.13)

Здесь S = pR² - площадь контура. Выражение 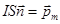(13.14)

называют магнитным моментом тока. Поле на оси кругового тока изменяется так же, как поле на оси электрического диполя (формула 3.34).

На достаточно большом расстоянии, когда r >> R, магнитное поле кругового тока, выглядит так же, как поле магнитного диполя, то есть двух одинаковых по величине и разных по знаку магнитных зарядов, лежащих на оси кругового тока по разные стороны его центра точки О. Поэтому взаимодействие полюсов постоянных магнитов, чьи поля создаются круговыми атомными токами, подчиняются закону Кулона для магнитных зарядов (формула 12.1). Измерив силу взаимодействия двух контуров с током, можно ввести единицу измерения этих условных магнитных зарядов.

Пример 13.5. Поле короткого соленоида. Коротким называется соленоид, чья длина соизмерима с его диаметром. Вычисление циркуляции вектора В здесь так же представляет сложную задачу, поскольку индукция В изменяется не только в окрестности концов, но и вдоль оси соленоида.

Вычислим индукцию поля в произвольной точке О оси соленоида радиусом R (рис.89), воспользовавшись формулой осевого поля кругового тока (пример 13.4).

Участок соленоида длиной dl вдоль оси эквивалентен элементу кругового тока IN₀dl, где N₀- число витков, приходящееся на единицу длины соленоида. Индукция поля dB, создаваемого этим элементом тока на оси соленоида в произвольной точке О, выразится формулой (13.13), где вместо тока I нужно подставить выражение IN₀dl.

. (13.15)

Здесь n - единичный вектор, направленный вдоль оси соленоида и согласованный с током.

Индукция в точке О, создаваемая всеми витками соленоида, найдётся интегрированием по всей его длине.

Выберем в качестве переменной интегрирования угол b между радиусом r и осью соленоида (рис.89). Тогда 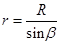, 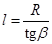. Отсюда 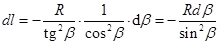. Подставляем в (13.15) и интегрируем вдоль оси x слева направо от точки A к точке C.

. (13.16)

Здесь b₁ - угол между осью соленоида и направлением из точки О в точку А, b₂- угол между осью и направлением в точку С. Если катушка очень длинная, то можно считать, что b₁ = 0, b₂ = p. Тогда формула (13.16) переходит в формулу индукции поля внутри бесконечно длинного соленоида (13.10). 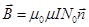. (13.17)

4. Магнитное поле одиночного движущегося заряда. Магнитное поле, создаваемое элементом тока Idl, логично рассматривать как сумму полей одиночных движущихся зарядов. Поэтому при малом отрезке dl можно записать: 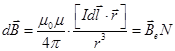. (13.18)

Здесь B_e индукция магнитного поля, создаваемого одиночным движущимся зарядом, N - число этих зарядов в элементе тока Idl. Так как 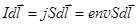, где e- величина движущихся в токе зарядов, n- их концентрация, v- скорость дрейфа зарядов, S-площадь поперечного сечения проводника, и приняв во внимание, что nSdl = N - число зарядов в элементарном проводнике, получаем: 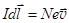. (13.19)

Знак вектора с элемента проводника dl перешёл на скорость дрейфа зарядов v. Это справедливо, поскольку направление вектора элемента тока Idl ещё в самом начале было определено через направление движения положительных зарядов.

Подставив выражение (13.19) в формулу (13.18) и разделив обе части равенства на число зарядов N, получаем полe одиночного движущегося заряда 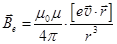. (13.20)

Можно сказать, что поле равномерно движущегося заряда определяется формулой Био-Савара-Лапласа, в которой вместо элемента тока Idl стоит произведение заряда на скорость его движения ev.