Замечание о несобственных двойных интегралах.
Точно так же, как и в определенных интегралах, вводят несобственные двойные интегралы двух типов: интеграл от непрерывной функции по неограниченной области (первого рода) и интеграл от разрывной функции по ограниченной области (второго рода).
Интеграл первого рода определяют как предел последовательности двойных интегралов от непрерывной функции по «расширяющимся» областям, стремящимся к заданной неограниченной области. Если предел существует и конечен, то интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.
Интеграл второго рода[6] определяют как предел последовательности интегралов от непрерывной функции по «расширяющимся» областям, стремящимся к заданной области и исключающим точку разрыва. Если предел существует и конечен, то интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.
Пример. Показать, что несобственный интеграл первого рода 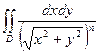 по области
по области 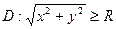 сходится при
сходится при 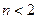 и расходится при
и расходится при 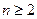 .
.
Показать, что несобственный интеграл первого рода 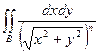 по области
по области 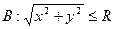 сходится при
сходится при 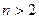 и расходится при
и расходится при 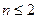 .Вычислим этот интеграл по области
.Вычислим этот интеграл по области 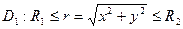 .
.
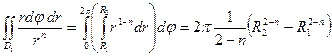 .
.
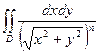 =
= 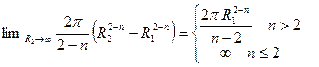
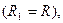
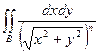 =
= 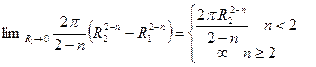
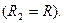
Часто расширение математических знаний позволяет решать задачи, которые не получались старыми методами.
Пример. Вычислить интеграл Пуассона 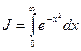 .
.
Неопределенный интеграл 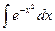 «не берется». Но двойной интеграл по области
«не берется». Но двойной интеграл по области 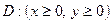 равен
равен
I = 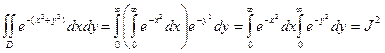 .
.
С другой стороны, переходя к полярным координатам, получим
I = 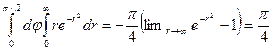 .
.
Поэтому 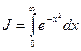 =
= 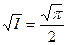 . По четности
. По четности 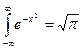 .
.
Дата добавления: 2017-11-21; просмотров: 1070;











