Замена переменных в кратных интегралах.
Исследуем общий случай замены переменных на примере двойного интеграла.
Пусть в области D задана непрерывная функция z = f(x,y), каждому значению которой соответствует то же самое значение функции z = F(u, v) в области D΄, где
F(u, v) = f(φ(u, v), ψ(u, v)). (25.12)
Рассмотрим интегральную сумму
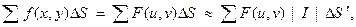
где интегральная сумма справа берется по области D΄. Переходя к пределу при 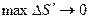 , получим формулу преобразования координат в двойном интеграле:
, получим формулу преобразования координат в двойном интеграле:
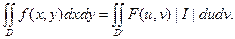 (25.13)
(25.13)
Аналогичным образом можно вывести подобную формулу для тройного интеграла:
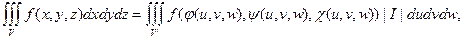 (25.14)
(25.14)
где x = φ(u, v, w), y = ψ(u, v, w), z = χ(u, v, w),
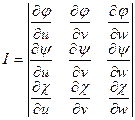 , (25.15)
, (25.15)
а область V пространства Оxyz отображается в область V΄ пространства Ouvw.
Переход к цилиндрическим и сферическим координатам
В тройном интеграле.
Найдем, используя формулы (25.6), (25.7) и (25.15), якобианы перехода от декартовых координат к цилиндрическим и сферическим:
1) для цилиндрических координат
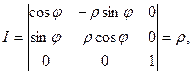 (25.16)
(25.16)
2) для сферических координат
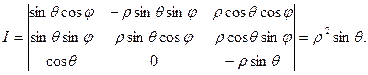 (25.17)
(25.17)
Тогда формулы перехода к цилиндрическим или сферическим координатам в тройном интеграле будут выглядеть так: (25.18)
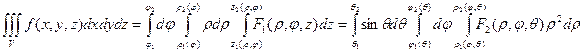 ,
,
где смысл обозначений понятен из предыдущего текста.
Примеры.
- Вычислим интеграл от функции
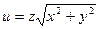 по области, ограниченной поверхностями x² + y² = 1, y = 0, y = x, z = 0, z = 1.
по области, ограниченной поверхностями x² + y² = 1, y = 0, y = x, z = 0, z = 1.
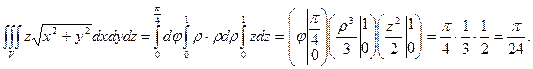
- Пусть подынтегральная функция u = 1, а область интегрирования – шар радиуса R с центром в начале координат. Тогда
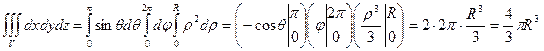 .
.
Дата добавления: 2016-06-18; просмотров: 4004;











