Задача о массе пространственного тела.

Пусть есть некоторое пространственное материальное тело, занимающее область V, в каждой точке которой задана объемная плотность f(x, y, z). Надо вычислить массу пространственного тела.

Эта задача приводит к понятию тройного интеграла.

Введем разбиение области V на элементарные области, не имеющие общих внутренних точек (условие А) Dv_k с малым объемом 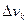(обозначение области и ее объема обычно одно и то же, это принято уже более 200 лет и не вносит путаницы).

На каждом элементе разбиения – элементарной области отметим точку M_k(x_k, y_k, z_k). Вычислим плотность в этой точке f(x_k, y_k, z_k) = f(M_k) и предположим, что плотность постоянна в элементарной области. Тогда масса элементарной области Dv_k приближенно равна 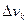= f(M_k) 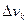. Суммируя все такие массы элементарных областей (составляя интегральную сумму), приближенно получим массу области V

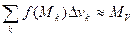
Для того, чтобы точно вычислить массу области, остается перейти к пределу при условии 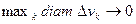(условие B).

.

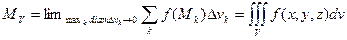Так задача о массе пространственной области приводит к тройному интегралу[7].

Введем некоторые ограничения на область интегрирования и подинтегральную функцию, достаточные для существования интеграла[8].

Потребуем, чтобы функция f(M) была непрерывна в области V и на ее границе.

Потребуем, чтобы область V была замкнутой, ограниченной, пространственно-односвязной областью с кусочно-гладкой границей.

Область назовем пространственно-односвязной, если ее можно непрерывной деформацией стянуть в точку.

Теорема существования.Пусть область V и функция f(M)=f(x, y, z) удовлетворяют сформулированным требованиям. Тогда тройной интеграл существует как предел интегральных сумм.

.

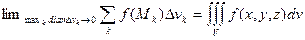Замечание. Предел этот не зависит[9]:

1) от выбора разбиения области, лишь бы выполнялось условие А

2) от выбора отмеченных точек на элементах разбиения

3) от способа измельчения разбиения, лишь бы выполнялось условие B.