Геометрический смысл несобственных интегралов с бесконечным пределом интегрирования

Несобственным интегралам можно придать смысл площади бесконечной фигуры.
Пример 1. Вычислить .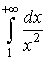
Решение. По определению имеем

.

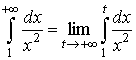Для нахождения интеграла, стоящего под знаком предела, воспользуемся формулой Ньютона-Лейбница

.

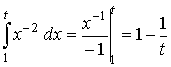Тогда

,

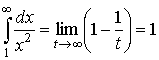т.е. искомый несобственный интеграл сходится к 1.
Аналогично, можно убедиться, что интеграл

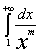
сходится к 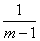, если m > 1, и расходящимся, если m ≤ 1.
Геометрический смысл этого результата состоит в том, что среди всех кривых вида 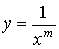гипербола 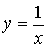является своеобразным "порогом". Если кривая данного вида на интервале [1; + ∞) лежит ниже гиперболы, то полубесконечная фигура имеет конечную площадь. Если же кривая лежит выше или совпадает с гиперболой 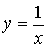, то соответствующая фигура имеет бесконечную площадь.

Пример 2. Вычислить .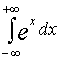
Решение. Исследуем на сходимость интегралы 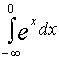и :

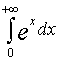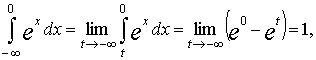
т.е. первый из интегралов сходится к 1. Но

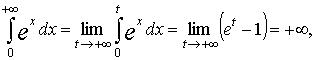
т.е. этот интеграл расходится и, следовательно, расходится несобственный интеграл .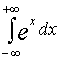

ВОПРОС 48. Признаки сходимости интегралов по бесконечным промежуткам.

Интегралы, получаемые двукратным переходом к пределу, называются несобственными.

_aò^∞f(x)dx=lim _aò^Rf(x)dx при R®∞.

Если такой предел существует, то говорят, что интеграл сходится.

ПРИМЕР:

Критерий Коши сходимости интеграла:

Чтобы несобственный интеграл по бесконечному промежутку сходился необходимо и достаточно, чтобы "e>0 $R(e) то есть R,R^’>R(e)Þ ê_Rò^Rf(x)dx÷=

ê(_aò^R’-_aò^R)f(x)dx÷<e.

Абсолютная и условная сходимости:

ü Если интеграл модуля функции по бесконечному промежутку сходится, то говорят, что интеграл абсолютно сходится.

ü Если интеграл модуля функции по бесконечному промежутку расходится, а интеграл этой функции по этому же промежутку сходится, то такой интеграл сходится условно.

Признаки сравнения:

Если çf(x)ú£g(x) и _aò^∞g(x)dx – сходится, то _aò^∞êf(x)çdx – абсолютно сходится.

Доказательство:

g(x)>0, _Rò^R’çf(x)dx÷£_Rò^R’g(x)dx<eÞ_Rò^R’çf(x)dxç - сходится.

ВОПРОС 49. Интегралы от разрывных функций. Признаки сходимости интегралов от разрывных функций.

Несобственный интеграл от разрывных функций

Ранее обозначенная формулировка определенного интеграла не может быть использована при существовании условий, когда функция 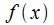на 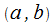является непрерывной, а при 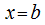имеет разрыв второго рода.

О: Под несобственным интегралом от функции 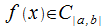, предполагающей наличие разрыва второго рода при 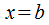, понимается 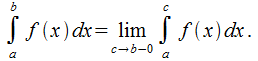Несобственный интеграл от функции 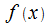, являющейся непрерывной и содержащей разрыв второго рода при 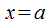, определяется как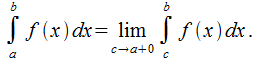

При условии, что существуют пределы и они являются конечными, интегралы можно назвать сходящимися, иначе — расходящимися.

О: Несобственный интеграл от функции 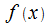, которая непрерывна на 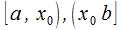и предполагает наличие разрыва второго рода при 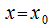- это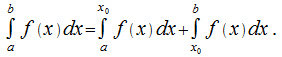

Сходимость интеграла существует при условии, что сходятся два интеграла справа, и отсутствует — если хотя бы один из них расходится.

Пример:

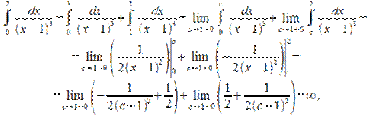
это означает, что интеграл расходится. Расходимость существует лишь при нс.и. от неограниченной функции.

ВОПРОС 50. Числовой ряд. Способы задания числовых рядов. Знакопостоянные числовые ряды.

ЧИСЛОВОЙ РЯД– бесконечная сумма членов бесконечной числовой последовательности {a_n}.

a1 + a2+ a3+ … + a_n+ … = .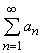

Каждому натуральному n сопоставляется сумма первых n членов последовательности {a_n}

S1 = a1, S2= a1 + a2, …, S_n = 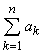= a1 + a2 + a3 + … + a_n, …

Значения S_n называют частичными суммами ряда. Они образуют последовательность {S_n} последовательностьчастичных сумм (бесконечного) ряда a_n – общий член ряда.

Если последовательность частичных сумм данного ряда имеет предел S,то есть

,

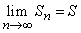то рядсходится и S – его сумма. Записывается это следующим образом:

a1 + a2 + a3 + … + a_n + … = S, или 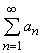= S.

В противном случае ряд называют расходящимся.

Таким образом, сумма ряда – это, по определению, предел последовательности его частичных сумм.

Пусть есть геометрическая прогрессия b_n = b1qⁿ–1, знаменатель которой qпо абсолютной величине меньше единицы (–1 < q < 1). Вычислим сумму первых n членов геометрической прогрессии:

S_n= b1+ b1qⁿ + b1q2 +…+ b1qⁿ–1= .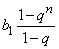

Очевидно, что при |q| < 1 с ростом n значение qⁿ стремится к нулю. Тогда значение S_n стремится к 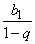и это число называетсясуммой всех членов бесконечной убывающейгеометрической прогрессии: b1 + b1qⁿ + b1q2 + …= .

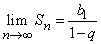Если все члены числового ряда имеют один и тот же знак, ряд называют знакопостоянным. Если все члены числового ряда имеют один и тот же знак, ряд называют знакопостоянным.

ВОПРОС 51. Сходимость ряда. Необходимое условие сходимости и достаточный признак расходимости знакопостоянного ряда. Свойства сходящихся числовых рядов.