Лекция 2. Приложения двойного интеграла.

Теорема.Пусть установлено взаимно однозначное соответствие областей D_xy и D_uv с помощью непрерывных, имеющих непрерывные частные производные функций 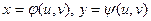. Пусть функция f(x,y) непрерывна в области D_xy. Тогда

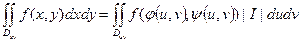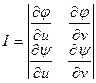, где - якобиан (определитель Якоби).

Доказательство (нестрогое). Рассмотрим элементарную ячейку в координатах u, v: Q₁, Q₃, Q₄, Q₂ – прямоугольник со сторонами du, dv. Рассмотрим ее образ при отображении 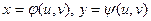- ячейку P₁, P₃, P₄, P₂.

P1 y x P3 P4 P2 Q1 Q2 Q4 Q3 v u

Запишем координаты точек Q1 (u, v), Q2 (u+du, v), Q3 (u, v+dv),

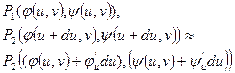
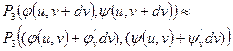
Приближенно будем считать ячейку P₃, P₄, P₁, P₂.параллелограммом, образованным сторонами 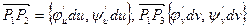. Вычислим площадь этой ячейки как площадь параллелограмма.

.

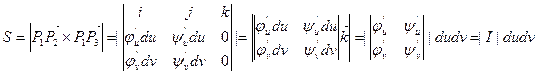Подставляя в интеграл площадь параллелограмма в качестве площади ячейки dxdy, получим .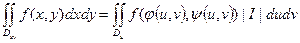

Следствие. Рассмотрим частный случай – полярную систему координат : . .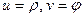

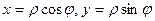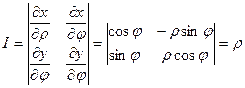Пример. Вычислить площадь внутри кардиоиды .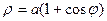

.

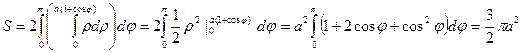Пример. Вычислить объем внутри прямого кругового цилиндра 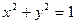, ограниченный плоскостью 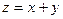в первом октанте.

.

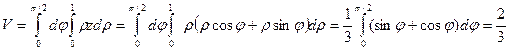Для каждой задачи можно выбрать ту систему координат, в которой вычисления проще. Декартова система координат удобна для прямоугольных областей. Если стороны прямоугольника параллельны координатным осям, то пределы интегрирования в повторном интеграле постоянны. Полярная система координат удобна для круга, кругового сектора или сегмента. Если центр круга находится в начале координат, то пределы интегрирования по углу и радиусу постоянны.