ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА. ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ

Интегрируя соотношение (13.50), получим

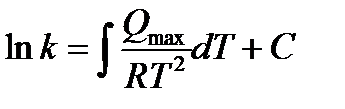, (13.51)

где С - константа интегрирования. Ее значение можно определить в случае, если для какой-либо температуры экспериментально найдены величины k и Q_max. После подстановки найденного значения С в формулу (13.51) она мо­жет быть использована для определения константы равновесия k при любой температуре.

Другой метод определения k основан на тепловой теореме Нернста, ле­жащей в основе третьего закона термодинамики. Используя эксперименталь­ные данные о состоянии конденсированных (твердых и жидких ) веществ, Нернст обнаружил, что разность 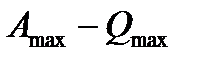является малой величиной и с приближением температуры к абсолютному нулю уменьшается быстрее, чем по линейному закону. Тогда из уравнения

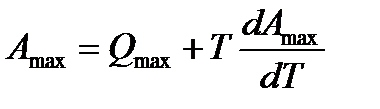
следует, что при 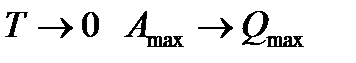.Следовательно,

.

Отсюда

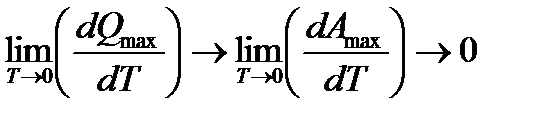. (13.52)

Соотношения (13.52) являются математическим выражением тепловой теоремы Нернста. Эти соотношения позволяют исключить константу интег­рирования С и получить зависимость 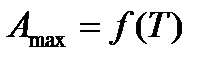аналитическим путем.

На основе этой теоремы можно заключить, что в уравнении Кирхгофа

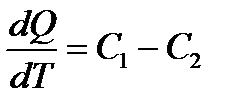
при 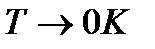разность теплоемкостей в правой части стремится к нулю. От­сюда следует, что и сами теплоемкости также стремятся к нулю.

ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ В ФОРМУЛИРОВКЕ ПЛАНКА (ПОСТУЛАТ ПЛАНКА)

Ранее было получено, что 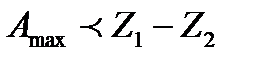(§ 13.9). Отсюда следует

.

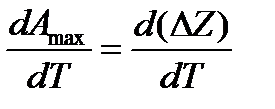Известно, что (§ 13.8)

.

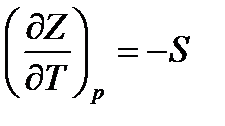Тогда

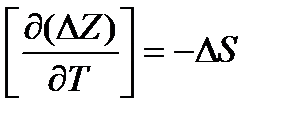
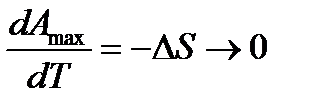. (13.53)

Из (13.53) следует, что с приближением температуры к 0 K все реакции протекают без изменения энтропии, а при Т = 0K энтропия конденсирован­ных систем равна нулю, т.е.

.

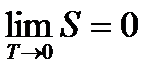Это происходит потому, что при приближении к абсолютному нулю тем­ператур образуется периодическая пространственная решетка, в которой ка­ждая молекула неподвижна. Т.е. происходит упорядочение взаимного распо­ложения молекул и уменьшение термодинамической вероятности w. И при абсолютном нуле температур w=l. Отсюда по формуле Больцмана

,

где 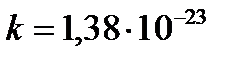Дж/(моль^.К) - константа Больцмана, получаем, что при 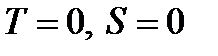. Это положение представляет собой третье начало термодинами­ки в формулировке Планка.

Третье начало термодинамики позволяет определить значение константы интегрирования в формуле (13.51) и, следовательно, абсолютное значение энтропии. При использовании дифференциальных уравнений термодинамики можно также определить абсолютные значения основных термодинамиче­ских функций F, Z и др.