СИСТЕМАХ И ХИМИЧЕСКИХ РЕАКЦИЯХ

<47 484950 51 52 53 >

Допустим, что в изолированной термодинамической системе, состоящей из двух подсистем, вещество находится в двух различных фазах, причем количество вещества в подсистемах изменяется при неизменном общем количестве вещества в системе, т.е.

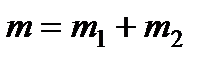. (13.34)

При постоянных температуре 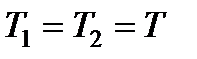и давлении 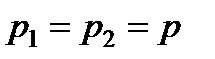изобарно-изотермический потенциал в условиях равновесия должен иметь минимум, т.е.

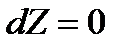. (13.35)

Ввиду аддитивности изобарно-изотермического потенциала

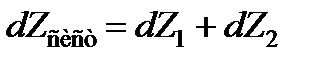. (13.36)

На основе соотношения (13.30)для 1-ой и 2-ой подсистем справедливы следующие равенства

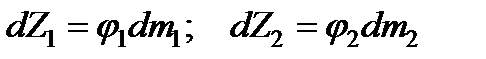. (13.37)

Подставляя (13.37)в (13.36)и учитывая, что в состоянии равновесия

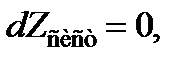получим

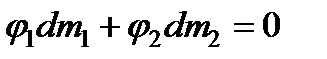С учетом (13.34) . Отсюда

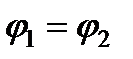
Таким образом, условия равновесия гетерогенной системы будут выполнены, если кроме равенства температур и давлений будет также выполнено условие равенства химических потенциалов фаз. А это означает, что в условиях равновесия удельные энергии в фазах равны.

Если число фаз больше двух, то в условиях равновесия при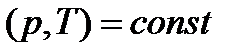

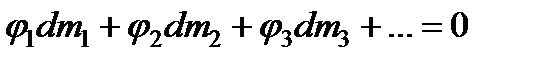
или

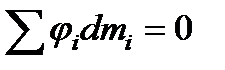. (13.38)

При равновесии в химических реакциях введение некоторого количества dn_i молей i-го компонента при сохранении постоянного количеств! молей всех других компонентов будет изменять значение изобарно-изотермического потенциала на величину

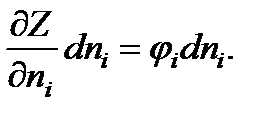
Отсюда уравнение

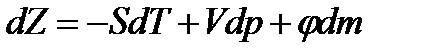
можно переписать в виде

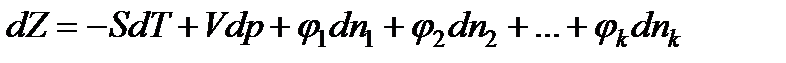
или

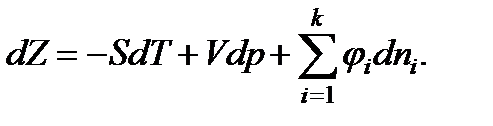
В условиях равновесия для химически реагирующих газов при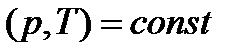

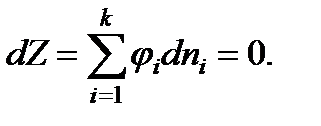(13.39)

Формула химического потенциала i - го компонента при условии, что он является идеальным газом, записывается в виде

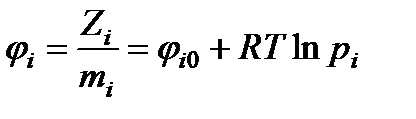, (13.40)

где Z_i - парциальное значение изобарно-изотермического потенциала i-го компонента в смеси; φ_i₀- значение химического потенциала i-го компонента,

не изменяющегося при постоянной температуре; p_i- парциальное давление i - го компонента.

<47 484950 51 52 53 >

Дата добавления: 2016-06-05; просмотров: 2041;