Уравнения в полных дифференциалах
Дифференциальное уравнение вида
P(x, y) dx + Q (x, y) dy = 0 (1)
называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции U(x, у), т.е.
P(x, y) dx + Q (x, y) dy = d U(x, у). (2)
Т.к. d U(x, у) = 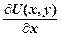 dx +
dx + 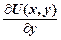 dy, то P(x, y) =
dy, то P(x, y) = 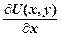 , Q (x, y) dy =
, Q (x, y) dy = 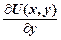 .
.
Уравнение (1) с учетом (2) можно записать в виде dU (x, y) = 0, поэтому его общий интеграл имеет вид
U (x, y) = С.(3)
Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие
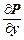 =
= 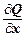 . (4)
. (4)
Имеются два основных способа решения уравнений в полных дифференциалах.
Первый способ.
Сначала проверяется условие (4). При его выполнении функция U (x, y)находится из системы уравнений 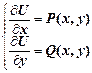 . (5)
. (5)
Пример 14. Решить уравнение у′ = 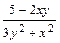 .
.
Запишем уравнение в дифференциальной форме (2ху – 5)dx + (3y2 + x2) dy = 0. Здесь P(x, y) = 2ху – 5,
Q (x, y) =3y2 + x2. Проверяем условие (4): 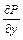 = 2х,
= 2х, 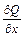 = 2х, т.е. условие (4) выполняется:
= 2х, т.е. условие (4) выполняется: 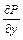 =
= 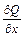 . Следовательно, исходное уравнение – уравнение в полных дифференциалах. Система (5) здесь имеет вид
. Следовательно, исходное уравнение – уравнение в полных дифференциалах. Система (5) здесь имеет вид 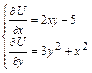 . Из первого уравнения имеем: U(x, y) =
. Из первого уравнения имеем: U(x, y) = 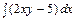 = x2y – 5x + φ(y) (6)
= x2y – 5x + φ(y) (6)
=> 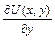 = x2 + φ′(y) . Сравниваем полученное выражение для
= x2 + φ′(y) . Сравниваем полученное выражение для 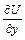 со вторым уравнением системы:
со вторым уравнением системы:
x2 + φ′(y) = 3y2 + x2 => φ′(y) = 3y2 => φ(y) = y3 + c1, т.е. (из (6)) U(x, y) = x2y – 5x + y3 + c1 =>
Общим интегралом исходного уравнения (см. (3)) является x2y – 5x + y3 + c1 = c2 или x2y – 5x + y3 = c,
где с = c2 – c1.
Второй способ.
Функция U (x, y)находится по формуле
U (x, y) = 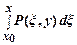 +
+ 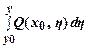 ,
,
где х0 и у0 – произвольные.
Пример 15. Решить уравнение (х – у) dx + ( 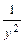 – x) dy = 0.
– x) dy = 0.
Проверяем условие (4): 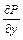 = –1,
= –1, 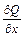 = –1, т.е. условие (4) выполняется:
= –1, т.е. условие (4) выполняется: 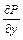 =
= 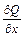 =>
=>
U (x, y) = 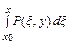 +
+ 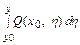 =
= 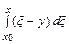 +
+ 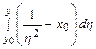 =
= 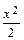 – yx –
– yx – 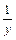 +
+ 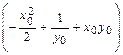 .
.
Т.к. х0 и у0 – произвольные постоянные, то выражение в скобках – const ( 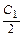 ). => U (x, y) =
). => U (x, y) = 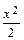 – yx –
– yx – 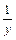 +
+ 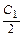 =>
=>
=> общий интеграл (U (x, y) = 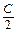 ):
): 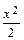 – yx –
– yx – 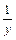 +
+ 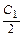 =
= 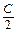 => х2у – 2у2х – 2 + Су = 0 (
=> х2у – 2у2х – 2 + Су = 0 ( 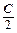 =
= 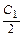 –
– 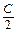 ).
).
Замечание. Если условие (4) не выполняется для уравнения (1), то в ряде случаев его можно свести к уравнению в полных дифференциалах умножением на некоторую функцию t (x, y) = t, называемую интегрирующим множителем.
Интегрирующий множитель легко находится в двух случаях: если t = t (x)или t = t (у):
В первом случае t (x)= 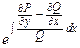 , причем выражение
, причем выражение 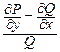 должно зависеть только от х;
должно зависеть только от х;
Во втором случае t (у)= 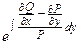 , причем выражение
, причем выражение 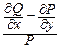 должно зависеть только от у.
должно зависеть только от у.
Пример 16. Решить уравнение (х2 – у) dx + (х2у2 + x) dy = 0.
Здесь 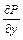 = –1,
= –1, 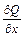 = 2ху2 + 1, т.е. условие (4) не выполняется:
= 2ху2 + 1, т.е. условие (4) не выполняется: 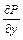 ≠
≠ 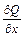 . Однако,
. Однако, 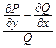 =
= 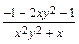 =
= 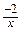
зависит только от х. Следовательно, уравнение имеет интегрирующий множитель, зависящий только от х, а именно, t(x)= 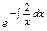 =
= 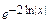 =
= 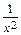 . Умножая исходное уравнение на t =
. Умножая исходное уравнение на t = 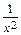 , получаем:
, получаем:
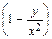 dx +
dx + 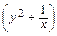 dy = 0, т.е. уравнение в полных дифференциалах. Решая его, найдем общий интеграл заданного уравнения х +
dy = 0, т.е. уравнение в полных дифференциалах. Решая его, найдем общий интеграл заданного уравнения х + 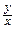 +
+ 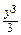 = С.
= С.
Дата добавления: 2017-11-21; просмотров: 1806;











