Уравнения Лагранжа и Клеро

<3 4 567 8 9 >

Некоторые дифференциальные уравнения первого порядка приходится решать методом введения вспомогательного параметра. К числу таких уравнений относятся уравнение Лагранжа

y = x j ( y¢) + y ( y¢)( 1 )

и уравнение Клеро

y = x y¢ + y ( y¢), ( 2 )

где j и y – известные функции от y¢.

Заметим, что оба этих уравнения не разрешены относительно производной y¢.

Уравнение Лагранжа (1) интегрируется следующим образом: обозначая р = y¢, запишем уравнение в виде

y = x j (р) + y (р). Дифференцируя полученное уравнение по х, имеем

Уравнение (1) может иметь особое решение вида y = x j(р₀) + y( р₀), где р₀ - корень уравнения р = j (р).

Уравнение Клеро является частным случаем уравнения Лагранжа при j ( y¢) = y¢. Его общее решение имеет вид у = Сх + y (С), особое решение получается путем исключения параметра р из уравнений у = рх + y (р) и

х = –y¢(р).

Пример 17. Решить уравнение Клеро у = ху′ + у′².

Общее решение (см. выше) имеет вид у = сх + с². Особое решение получается путем исключения параметра р из уравнений у = рх + р² и х = –2р: у = – 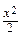+ 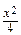, т.е. у = – .

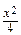Дифференциальные уравнения высших порядков

Основные понятия

Дифференциальное уравнение второго порядка в общем случае записывается в виде

F (x, y, y¢, y¢¢ ) = 0 ( 1 )

или в виде, разрешенным относительно старшей (второй) производной

y¢¢ = f (x, y, y¢ ). ( 2 )

Решением ДУ2 (1)–(2) называется любая функция у = j (х), которая при подстановке в это уравнение обращает его в тождество. График функцииу = j (х) называется интегральной кривой.

Задача отыскания решения ДУ(1)–(2), удовлетворяющего заданным начальным условиям у(х₀) = у₀, у¢ (х₀) = у¢₀, где х₀,у₀, у¢ ₀ – некоторые числа, называется задачей Коши. Геометрически это равносильно следующему: требуется найти интегральную кривую уравнения (1)–(2), проходящую через точку М(х₀, у₀) с угловым наклоном касательной в этой точке у¢₀.

Общим решением уравнения (1)–(2), называется функция у = j (х, С₁, С₂), зависящая от двух произвольных постоянных С₁ и С₂ и такая, что:

1) при любых конкретных значениях С₁ и С₂ она является решением этого уравнения;

2) для любых допустимых начальных условий

у(х₀) = у₀, у¢ (х₀) = у¢₀, ( 3 )

можно подобрать такие значения С₁⁰ и С₂⁰ постоянных, что функция у = j (х, С₁⁰, С₂⁰) будет удовлетворять этим начальным условиям.

Частным решением уравнения (1)–(2) называется функция у = j (х, С₁⁰, С₂⁰), получающаяся из общего решения при конкретных значениях постоянных С₁ и С₂.

Геометрически общее решение ДУ2 представляет собой множество интегральных кривых; частное решение – одну из интегральных кривых этого множества.

Теорема Коши – (существования и единственности решения ДУ2). Если в уравнении у′′ = f (x, y, y¢) функция f (x, y, y¢) и ее частные производные f ¢_у(x, y, y¢) и f ¢_у_¢(x, y, y¢) непрерывны в некоторой области D, содержащей точку с координатами (х₀, у₀, у¢₀), то существует и притом единственное решение у = у(х) этого уравнения, удовлетворяющее начальным условиям у(х₀) = у₀, у¢ (х₀) = у¢₀.

Аналогичные понятия и определения имеют место для ДУ n–го порядка, которое в общем виде записывается

F (x, y, y¢, y¢¢ , … , y⁽ⁿ⁾) = 0 или y⁽ⁿ⁾ = f (x, y, y¢, y¢¢ , … , y⁽ⁿ^–¹⁾).(4)

Начальные условия для ДУ(4):

y|_x₌_x₀ = y₀, y′|_x₌_x₀ = y′₀, y′′|_x₌_x₀ = y′′₀, … , , y⁽ⁿ^–¹⁾|_x₌_x₀ = y₀⁽ⁿ^–¹⁾.(5)

Общим решениемДУ n–го порядка называется функция вида у = j (х, С₁, С₂, … , С_n), содержащая n произвольных, не зависящих от х, постоянных.

Решение ДУ(4), получающееся из общего решения при конкретных значениях постоянных

С₁= С⁰₁, С₂= С⁰₂, … , С_n = С⁰_n, называется частным решением.

Задача Коши дляДУ n–го порядка: найти решение ДУ(4), удовлетворяющее начальным условиям (5).

Проинтегрировать (решить) ДУ n–го порядка означает следующее: найти его общее или частное решение (интеграл) в зависимости от того, заданы начальные условия или нет.

Задача нахождения решения ДУ n–го порядка сложнее, чем первого. Поэтому рассматриваем лишь отдельные виды ДУ высших порядков (≥ 2)

<3 4 567 8 9 >

Дата добавления: 2017-11-21; просмотров: 2424;