Однородные дифференциальные уравнения (ОДУ)

Функция f (x, y) называется однородной функцией степени n, где n – целое, еслипри любом t имеет место тождество f (tx, ty) = t ⁿ f (x, y).

В частности, функция f (x, y) однородная нулевой степени, если f (tx, ty) = f (x, y).

Дифференциальное уравнение вида

P(x, y) dx + Q (x, y) dy = 0 ( 1 )

называется однородным, если P(x, y) и Q (x, y) – однородные функции одинаковой степени.

Уравнение (1) может быть приведено к виду .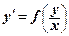

Однородное уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены переменной 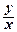= u, т.е. y = ux, где u = u (х) – новая неизвестная функция.

Имеем y = ux, y′ = u′x + u.

Подставляя эти выражения вместо у и у¢ в исходное уравнение, получим уравнение с разделяющимися переменными относительно переменной u. Решив его, окончательно получим решение в виде зависимости у от х: y = ux.

Замечание 1. Вместо подстановки y/x = u можно применять подстановку x/y = u.

Пример 8. Проинтегрировать уравнение = .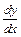

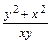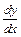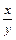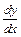Перепишем уравнение в виде = + . Положим u = , тогда = u + x 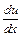, и уравнение

преобразуется к виду u + x 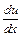= u + или u du = 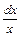. Интегрируя, получим u² = ln Cx²,

или у² = x² ln Cx².

Пример 9. Найти общий интеграл уравнение (х² – у²) dx + 2xy dy = 0.

Данное уравнение однородное, т.к. функции Р(х, у) = х² – у² и Q(х, у) = 2xy – однородные функции второго

порядка. Перепишем уравнение в виде 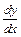= – 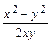или 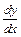= 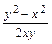. Разделив левую часть уравнения на

ху (в данном случае делим почленно числитель на знаменатель), получим 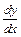= – 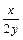. Положим u = ,

тогда 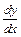= u + x 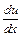, и уравнение преобразуется к виду u + x 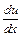= 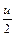– 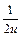или 2x = – .

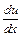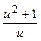Разделив переменные, получим 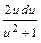= – 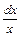. Интегрируем:ln (u² + 1) =– ln |х| + ln |C| => u² + 1 = .

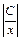Заменяя u на , придем к общему интегралу исходного уравнения х² + у² = Сх.

Замечание 2. Уравнение вида 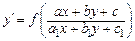приводится к однородному или с

разделяющимися переменными. Для этого вводят новые переменные u и v, положив

х = u + α, у = v + β, где α и β – числа. Их подбирают так, чтобы уравнение стало однородным.

Если 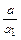= 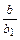, то исходное уравнение приводится к уравнению с разделяющимися переменными

подстановкой u = ax + by.

Пример 10. Найти общий интеграл уравнение (x + 2у + 1) dx – (2x + y – 1) dy = 0.

Перепишем уравнение в виде 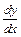= 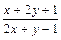. Положив х = u + α, у = v + β, получаем: dx = du, dy = dv;

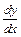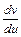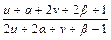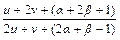= = = . Подберем α и β так, чтобы .

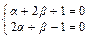Решением данной системы являются α = 1 и β = –1. Тогда заданное уравнение примет вид 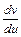= 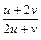и

будет однородным => решаем его: 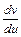= =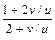> || v/u = t => v = tu => v′_u = t + u t′_u || => t + u t′_u =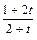

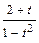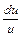=> t′_u = => dt = => ln 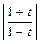– 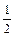ln | 1 – t² | = ln | u | + ln | C | => = u C =>

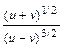=> = C => x + y = C (x – y – 2)³.