Линейные уравнения. Уравнения Бернулли
Дифференциальное уравнение вида
у¢ + р(х) у = q(x), ( 1 )
где р(х) и q(x) – непрерывные функции (в частности – постоянные), называется линейным уравнением первого порядка.
Особенность данного типа уравнений: искомая функция у и ее первая производная у′ входят в уравнение в первой степени, не перемножаясь между собой.
Замечание 1. Уравнение вида a(х) у¢ + b(х) у = c(x) легко сводится к уравнению вида (1) делением на a(х).
Замечание 2. Уравнение вида х¢ + p(y) x = q(y) является линейным относительно х и х¢.
Если q(x) º 0,то уравнение (1) принимает вид
у¢ + р(х) у = 0, ( 2 )
и называется линейным однородным. Оно является уравнением с разделяющимися переменными. В случае q(x) ¹ 0уравнение (1) называется линейным неоднородным уравнением.
МЕТОД И.БЕРНУЛЛИ
Решение уравнения (1) ищется в виде y = uv, где u = u(x) и v = v(x) – неизвестные функции от х (метод Бернулли). При этом одну из функций (например, v(x)) можно выбрать произвольно (из соображений удобства), тогда вторая определится из уравнения (1). В обоих случаях они находятся из уравнений с разделяющимися переменными.
Пример 11. Проинтегрировать уравнение у′ +2ху =2x.
Это линейное неоднородное уравнение. Решаем его методом Бернулли (говорят, методом « u на v»): решение ищем в виде y = uv, тогда y′ = u′v + uv′ и исходное уравнение преобразуется к виду u′v + uv′ +2хuv =2x. Запишем его в виде u′v + u(v′ +2хv)=2x.
1) Найдем функцию v, превращающую выражение в скобках в нуль. Для этого решим диф.уравнение v′ +2хv = 0.
Имеем 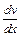 = –2хv =>
= –2хv => 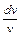 = –2хdx => ln |v|= –х2 (ввиду произвольности выбора v, С берем равным таким, каким нам удобно; в данном случае С = 0) => v =
= –2хdx => ln |v|= –х2 (ввиду произвольности выбора v, С берем равным таким, каким нам удобно; в данном случае С = 0) => v = 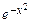 .
.
2) Т.к. при полученном v v′ +2хv = 0, то теперь решаем уравнение u′v =2x, т.е. u′ 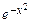 =2x. Имеем:
=2x. Имеем:
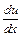
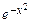 =2х => du =2х
=2х => du =2х 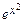 dx => u =
dx => u = 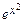 + C.
+ C.
3) Т.о., окончательно общее решение имеет вид y = uv =( 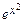 + C) ∙
+ C) ∙ 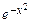 =1 + С
=1 + С 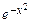 .
.
Дата добавления: 2017-11-21; просмотров: 1465;











