Не содержащие явно независимой переменной х

Уравнения такого вида допускают понижение порядка подстановкой y¢= р = р(у).Тогда

у¢¢ = 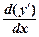= = 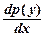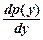∙ 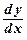= 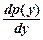∙ р, т.е. у¢¢ = р¢р .

Уравнения (10) сводятся т.о. к ДУ 1-го порядка р ∙ 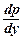= f (y, p). Пусть p = φ ( у, С₁) –общее решение полученного ДУ первого порядка. Заменяя функцию р на y¢, получим y¢ = φ ( у, С₁). Это уравнение с разделяющимися уравнениями. Интегрируя его, найдем общий интеграл уравнения (10): 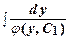= х + C₂.

Частным случаем уравнений (10) являются уравнения F ( y, у¢¢) = 0или у¢¢ = f ( y ) .

Они интегрируется тем же способом: y¢= р(у),у¢¢ = .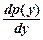

Так же поступаем при решении уравнения вида

F ( у, y^(k), y^{(k + 1 )}, … , у⁽ⁿ⁾ ) = 0или у⁽ⁿ⁾ = f ( у, y^(k), y^{(k + 1 )}, … , у^{(n – 1)}).

Их порядок его можно понизить на единицу, положив y¢= р(у).Как уже показано, у¢¢ = р ∙ 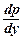.Далее, у¢¢¢ = 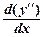= 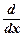( р ∙ р¢_у) = 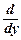( р ∙ р¢_у) ∙ 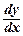= р ∙ ((р¢_у)² + р ∙ р¢¢_уу)и т.д.

Замечание. Уравнения (8) также можно решать, применяя подстановку y¢= р(у), у¢¢ = р¢р .

Пример 3. Найти частное решение уравнения у′′ – (у¢ )²+ у¢ (у – 1)= 0, удовлетворяющее

начальным условиям у(0) = 2, у¢ (0) = 2.

Уравнение имеет вид (10). Полагая у′ = р(у), у′′ = р 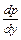, получаем р 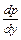– р²+ р (у – 1)= 0. Т.к. р ≠0 (иначе у¢ = 0, что противоречит условию у¢ = 2), то 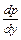– р + (у – 1)= 0 – получили линейное ДУ 1-го порядка. Решаем его методом Бернулли («u на v»): p = u ∙ v . Уравнение примет вид u′ v + u v′ – u v + у – 1= 0 или

u′ v + u (v′ – v)= 1 – у. Подберем функцию v так, чтобы v′ – v = 0: 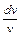= dy => v = e ^y. Далее, u′ e ^y = 1 – у, т.е.

du =(1 – у) e ^–y dy. Интегрируя это равенство, находим, что u =–(1 – у) e ^–y + e ^–y + C₁. Следовательно,

p = u ∙ v = ( (–1 + у) e ^–y + e ^–y + C₁) ∙ e ^y. Заменяя р на у′, получаем у′ = C₁ e ^y + у. Подставляя у¢ = 2 и

у = 2 в это равенство, находим C₁: 2= C₁ e ² + 2 => C₁ = 0. Имеем: у¢ = у . Отсюда у = C₂ e ^х . Находим C₂ из начальных условий: 2= C₂ e ⁰ => C₂ = 2. Т.о., у =2 e ^х – частное решение исходного ДУ с заданными начальными условиями.

2.4. Уравнения вида F ( х, у, y¢, у¢¢) = 0, где F ( х, у, y¢, у¢¢) – однородная функция относительно переменных у, y¢, у¢¢

Пусть F ( х, tу, ty¢, tу¢¢) = t ^k F ( х, у, y¢, у¢¢).Тогда диф.уравнение F ( х, у, y¢, у¢¢) = 0допускают понижение порядка подстановкой у = 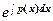, где р(х) – новая неизвестная функция.